凸优化2021-09-21
背景知识
函数符号解释
:在集合中改变,求的最小值
:函数是关于两个变量的函数,该式的含义是固定不变,改变从而使得函数最小
,该式的含义是:
- 是关于的函数
- 当时,的取值为:固定中的,改变使函数取到最小值。例如:
,从右向左看,将理解成关于的函数,然后再对求最大值,即:
和
:下确界(infimum)
:上确界(supremum)
和min、max有相似之处,细节略有不同。示例:
对函数,在处,不存在,但存在且为1。
拉格朗日乘子法
凸函数
下图为凸函数图像示例:
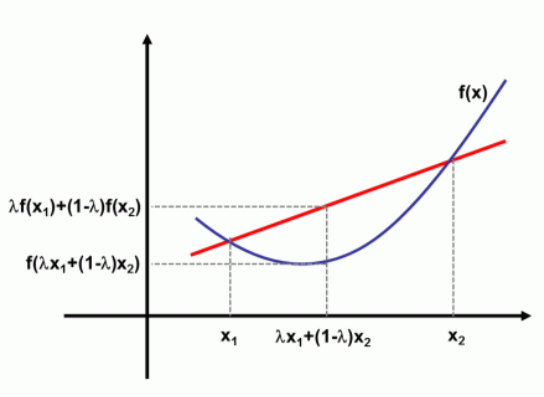
若函数是凸的,则:
若函数是凹的,则:
仿射函数
假设有,,那么:
被称为的仿射变换,该过程称为仿射函数:
例如,以下为简单的仿射函数:
仿射函数的重要性质:既凹且凸,即在凹凸函数不等式中,仿射函数可以取等号。
其它符号
- :函数的定义域
- :集合的交集
无约束
求导,令导数为0即可。
等式约束
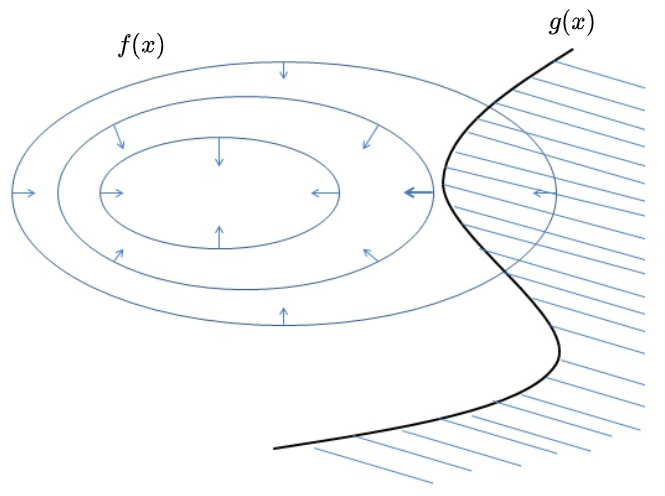
问题如下:
交点:移动时会导致增大或减小,因此不是可行解。
切点:可能是极值点(在其邻域内,此值最大),此时满足。
构造朗格朗日函数:
将对和求偏导可得:
求解以上方程即可。
不等式约束(KKT条件)
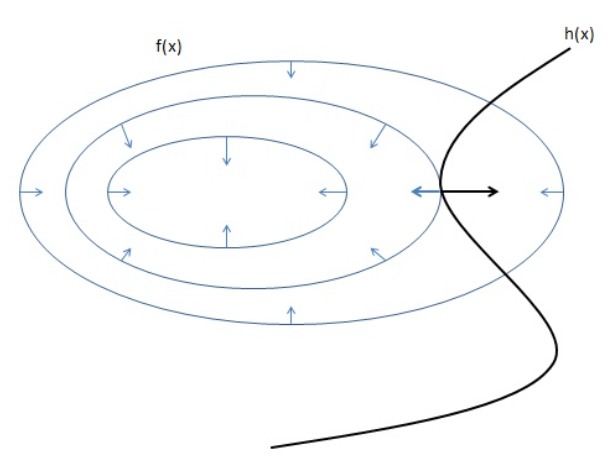
问题如下:
假设函数的右侧小于0,即阴影部分为约束的可行域。函数向内侧为等高线数值降低方向。两种情况如下:
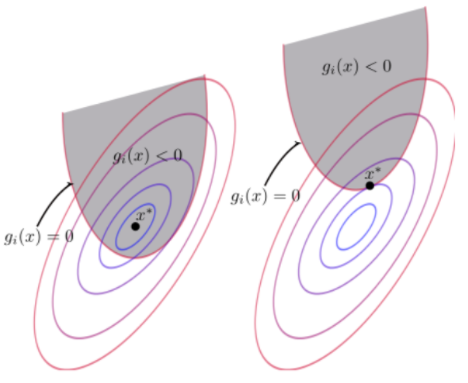
将以上两种情况进行合并,得:
这个方程组就是该问题的 KKT 条件,只有满足这些条件才会存在极小值。
情况二中,为什么大于等于0?
因为梯度方向指向函数增大方向,因此的梯度指向左侧,而的梯度指向右侧,因此两个函数的梯度方向相反。
对偶问题
原始问题
假设是定义在上的连续可微函数。
定义如下的约束最优化问题为原始优化问题或原问题:
此处,不假定函数的凹凸性,即可以是非凹非凸函数。
原问题直接优化比价困难:
1. 约束条件太多,总共个约束
2. 原问题凹凸性不明确
而对于原问题的拉格朗日对偶问题,其优点为:
1. 只有1个约束。
2. 拉格朗日对偶为一定是凹的。
引入拉格朗日函数:
其中,、是拉格朗日乘子, 构建关于的函数:
假设给定某个违反原始问题约束条件的,即存在某个使得或。若,可令,使得;若,可令或,使得。将其余均置为0。那么:
假设给定某个符合原始问题约束条件的,即且,那么:
由以上分析,得:
,满足原始问题约束,不满足原始问题约束 则极小化如下原始问题等价于原始最优化问题,即有相同的解:
称为广义拉格朗日函数的极小极大问题。
定义原始问题的最优值:
称为原始问题的最优解。
对偶问题
构建关于的拉格朗日对偶函数:
对偶函数重要性质:
- 对偶函数一定是凹函数。
- 在的条件下,的值不会超过原问题的解,即。启示:当不容易求解的时候,可以求解进行逼近。
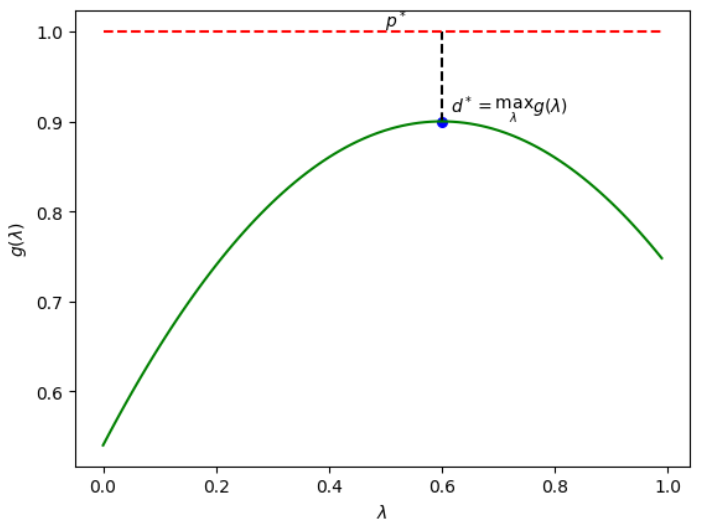
对偶函数极大化问题称为广义拉格朗日函数的极大极小问题:
将广义拉格朗日函数的极大极小问题表示为约束最优化问题,称为原始问题的对偶问题:
定义对偶问题的最优值,称为对偶问题的解:
定理若原始问题和对偶问题都有最优解,则
证明:对任意的,和,有:
即:
由于原始问题和对偶问题均有最优值,所以:
即:
问题得证。
原始问题和对偶问题的关系
如果满足KKT条件或slater条件,则。并且,能够通过对偶问题的解,得到原问题的解!
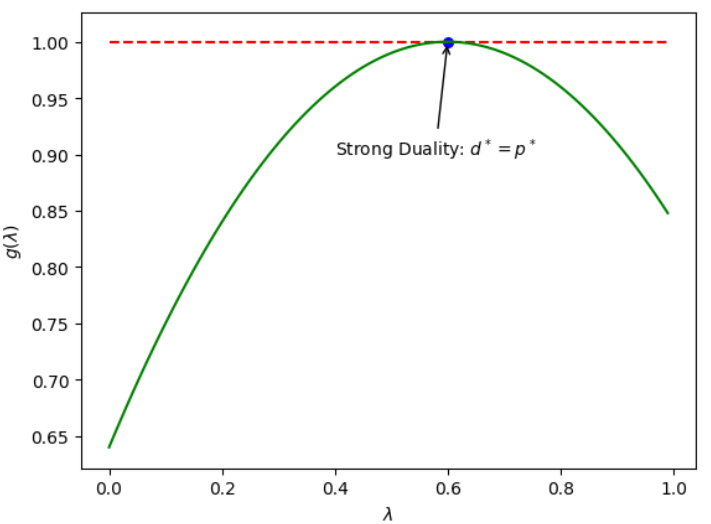
原始问题:
对偶问题:
定理对原始问题和对偶问题,假设函数和是凸函数,是仿射函数,并且不等式约束是严格执行的,则和,分别是原始问题和对偶问题的解的充分必要条件是,,满足下面的条件:
定理概括:条件,,是原始问题和对偶问题的解。
定理部分解释:
是严格执行的:严格满足
条件1 & 条件2:原始问题约束条件
条件3:对偶问题的必要条件,参考公式()对偶函数定义
条件4:如果满足该条件,那么必然是函数的最优解,即原问题的解。那么,如何证明,是对偶问题的解???
条件5:又称互补松弛条件。如果,,是原始问题和对偶问题的解,则。证明如下:
假设,那么可知,是函数的最小值,是函数的最大值
假设当前的凸优化问题满足强对偶条件,那么:,所以,。
根据定义:
在满足约束的条件下
又
对偶问题求解总结
使用对偶方法求解最优化问题步骤:
确定原始问题
构造拉格朗日函数
其中,、是拉格朗日乘子, 构造拉格朗日对偶函数
求解拉格朗日对偶函数
对偶函数极大化
例题
解:1. 构造拉格朗日函数:
2. 构造对偶函数:
3. 求解对偶函数:
解得:
所以,
4. 对偶函数极大化:
可求得:
5. 求
由于 ,通过对偶函数的解可以求得原函数的解,因此:
参考资料
- 人工智能数学基础——第五章 最优化 -3约束最优化 - 知乎 (zhihu.com)
- 拉格朗日乘子法,KKT条件,对偶问题 - 知乎 (zhihu.com)
- 拉格朗日对偶性 - 知乎 (zhihu.com)
- (56条消息) 【数学】拉格朗日对偶,从0到完全理解frostime的博客-CSDN博客拉格朗日对偶
- Karush-Kuhn-Tucker (KKT)条件 - 知乎 (zhihu.com)