无约束优化2022-08-27
符号定义
:训练样本数目
:训练样本
:label
:参数向量
:损失函数,以平方损失为例,
:第个训练样本的损失函数,以平方损失为例,
:时间步
:第个时间步的参数的梯度,以平方损失函数为例
:函数的梯度
方向导数
方向导数定义
设在的某邻域内有定义,是平面上一个单位向量,若存在,则该极限值就是在点沿方向的方向导数,记作
若可微,则
陷阱:上述公式仅限于可微前提下,若不可微,必须回归方向导数的定义。
方向导数与偏导数的关系
方向导数定义:
偏导数定义:
所以:
当时,方向导数当时,方向导数 结论:
是沿方向的方向导数,是沿方向的方向导数。
梯度
在处可微,梯度定义如下:
梯度与方向导数的关系
在可微的前提下:
其中,为与之间的夹角 结论:沿梯度方向的方向导数最大,由于导数为正,函数递增,因此在的邻域内沿梯度方向函数增加最快,沿负梯度方向函数减小最快。
梯度与等高线的关系
结论:梯度垂直于等高线的切线。
梯度下降法
设损失函数为,优化目标为:
则使用梯度下降法求解的步骤为:
假设有个样本点,特征值为,真实值为,预测值为,定义损失函数为,那么,参数的更新公式为:
因此,梯度下降的时间复杂度是。
随机梯度下降法
相比于梯度下降使用全量数据更新梯度,随机梯度下降法基于均匀分布每次选择一个样本更新梯度,时间复杂度由降为。
小批量梯度下降法
介于梯度下降法和随机梯度下降法之间,每次使用均匀分布选择个训练样本组成小批量,其时间复杂度为。
梯度下降算法的缺点
- 下降速度慢
- 可能会在沟壑两边持续震荡,停留在一个局部最优点
动量法
其中,为一阶动量,为超参数,为损失函数的一阶梯度,为学习率 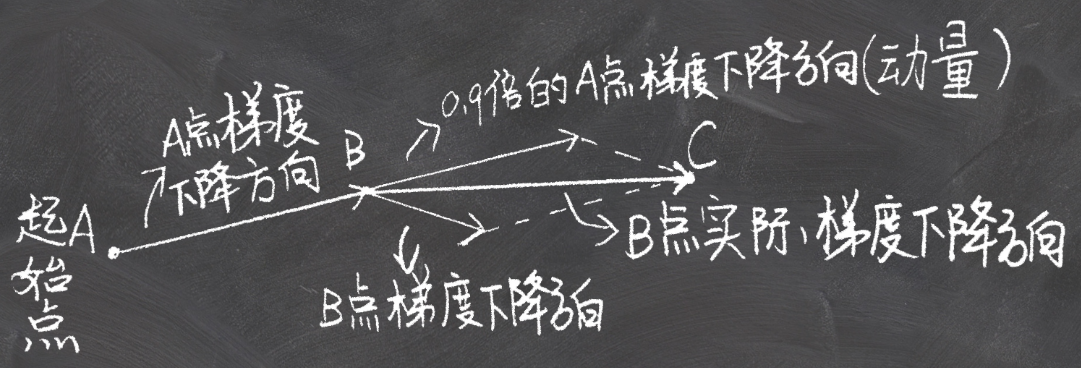
假设起始点为A,起始点的动量初始化为0:
- A -> B:方向为 点A的负梯度方向
- B -> C:方向为 点B的负梯度方向+点A的梯度方向
NAG(Nesterov Accelerated Gradient)
其中,为一阶动量,为超参数,为损失函数的一阶梯度,为学习率
牛顿法
零点求解
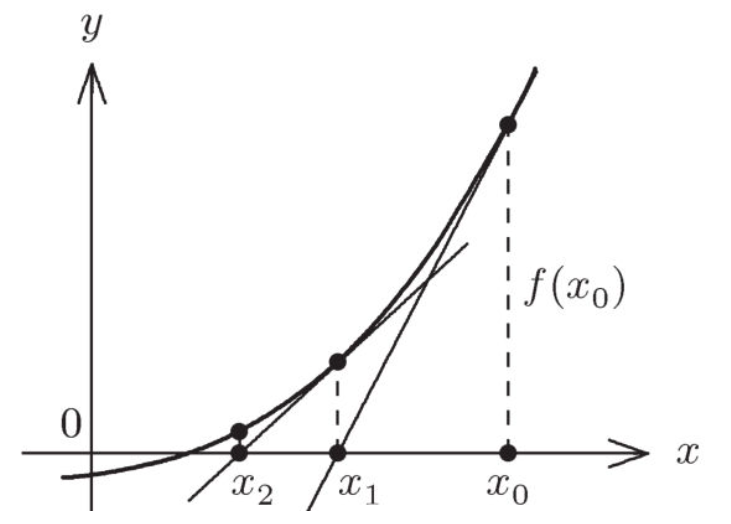
求解目标:
迭代步骤:
初始点过点做的切线方程,则方程为,化简得:求切线与轴的交点:由此,得到迭代公式:按照迭代公式进行迭代,直到满足阈值要求
牛顿迭代法执行步骤示例:
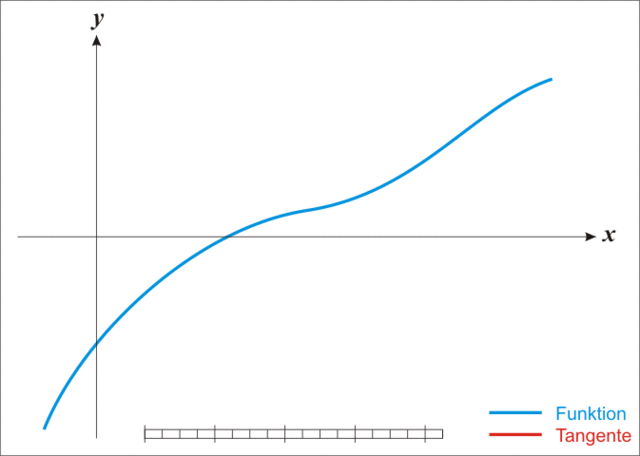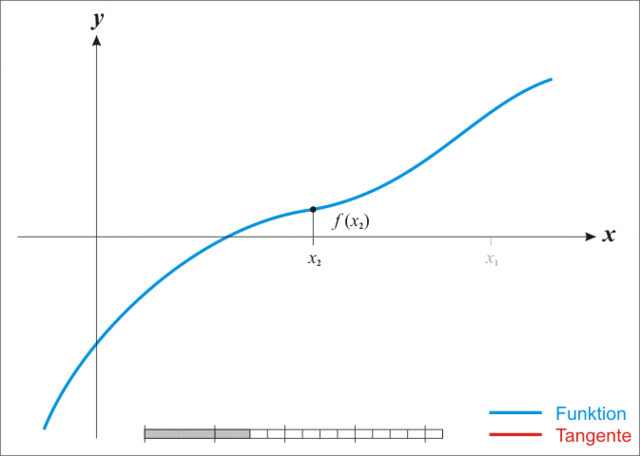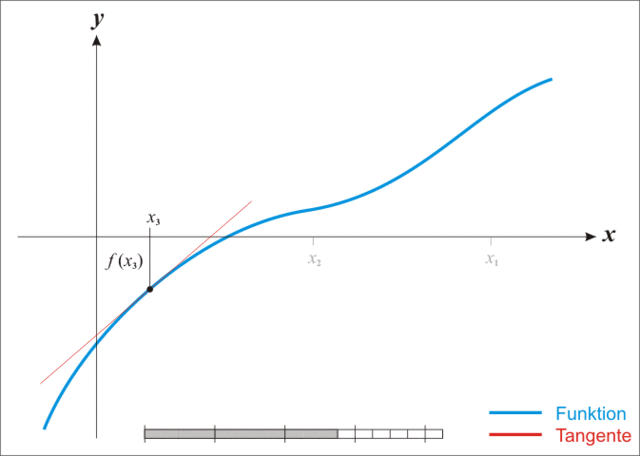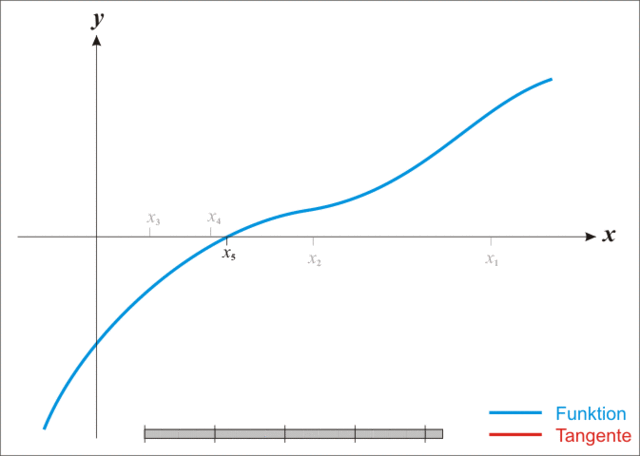
牛顿法
设损失函数为,优化目标为:
假设的极小值点存在,则求的最小值等价于求的点。
令,根据牛顿迭代法,如果要求的点,则迭代公式为:
AdaGrad
在时间步,AdaGrad将中的每个元素都初始化为0
在时间步,首先将小批量随机梯度按元素平方和累加到变量:
其中,是按元素相乘 将目标函数自变量中每个元素的学习率通过按元素运算重新调整:
其中,是学习率,是为了维持数值稳定性而添加的常数,如 一直在累加按元素平方的小批量随机梯度,所以目标函数自变量每个元素的学习率在迭代过程中一直在降低(或不变)。因此,当学习率在迭代早期降得较快且当前解依然不佳时,AdaGrad算法在迭代后期由于学习率过小,可能较难找到一个有用的解。
RMSProp
在时间步时,
其中,为超参数,为学习率是为了维持数值稳定性而添加的常数,如 因为RMSProp算法的状态变量是对平方项的指数加权移动平均,因此可以看作是最近个时间步的小批量随机梯度平方项的加权平均。因此,自变量每个元素的学习率在迭代过程中就不再一直降低(或不变)。
AdaDelta
在时间步时,所有元素被初始化为0,状态变量所有元素被初始化为0
在时间步时:
计算自变量的变化量:
其中,是为了维持数值稳定性而添加的常数,如 更新自变量:
使用来记录自变量变化量按元素平方的指数加权移动平均:
可以看到,如不考虑的影响,AdaDelta算法跟RMSProp算法的不同之处在于使用来代替学习率。
Adam
Adam = Adaptive+Momentum
在时间步,将和初始化为0
在时间步,
其中,和为超参数,建议为,建议为 无偏修正:
更新参数:
NAdam
NAG回顾与改写
回顾NAG的公式:
其中,为一阶动量,为超参数,为损失函数的一阶梯度,为学习率 NAG的核心在于,计算梯度时使用了未来位置: 。NAdam中提出了一种公式变形的思路,可以理解为:只要能在梯度计算中考虑到未来位置,即能达到 Nesterov 的效果。既然如此,那么在计算梯度时,可以仍然使用原始公式进行计算,但在计算时,使用未来时刻的动量,即,那么理论上所达到的效果是类似的。
理论上,下一刻的动量为:
在假定连续两次的梯度变化不大的情况下,那么:
此时,可使用近似表示未来动量,加入到的迭代公式中。
因此,原始NAG的公式可以修改为:
其中,为一阶动量,为超参数,为损失函数的一阶梯度,为学习率 NAdam
类似的,在Adam可以加入的变换,将Adam中的展开有:
引入替换(与Adam的不同之处):
再进行更新:
常见问题
为什么深度学习不使用牛顿法或者拟牛顿法?
- 牛顿法需要用到梯度和Hessian矩阵,这两个都难以求解。因为很难写出深度神经网络拟合函数的表达式,遑论直接得到其梯度表达式,更不要说得到基于梯度的Hessian矩阵了。
- 即使可以得到梯度和Hessian矩阵,当输入向量的维度N较大时,Hessian矩阵的大小是N×N,所需要的内存非常大。
- 在高维非凸优化问题中,鞍点相对于局部最小值的数量非常多,而且鞍点处的损失值相对于局部最小值处也比较大。而二阶优化算法是寻找梯度为0的点,所以很容易陷入鞍点。
如何选择合适的优化算法?
参考文档
通俗理解 Adam 优化器 - 知乎 (zhihu.com)
Adam那么棒,为什么还对SGD念念不忘?一个框架看懂深度学习优化算法 (qq.com)
https://www.zhihu.com/question/36301367
https://www.cnblogs.com/yanghh/p/13739024.html
SGD optimizer with momentum (dejanbatanjac.github.io)
Nesterov加速和Momentum动量方法 - 知乎 (zhihu.com)
(133条消息) Adam优化器偏差矫正的理解飞奔的帅帅的博客-CSDN博客adam偏差修正
(2 条消息) 深度学习中的优化算法 NAdam 和 Nesterov + Adam 有区别么、区别在哪? - 知乎 (zhihu.com)
深度学习优化算法(牛顿法-->梯度下降法-->Nadam) - liujy1 - 博客园 (cnblogs.com)
路遥知马力——Momentum - 知乎 (zhihu.com)
比Momentum更快:揭开Nesterov Accelerated Gradient的真面目 - 知乎 (zhihu.com)


