p-value概念

$H_0$$H_0$：Null Hypothesis，原假设

$H_1$$H_1$：Alternative Hypothesis，备择假设

$\alpha$$\alpha$：显著性水平，是指当原假设为正确时人们却把它拒绝了的概率或风险，即错判的概率。假设检验是围绕对原假设内容的审定而展开的。如果原假设正确我们接受了（同时也就拒绝了备择假设），或原假设错误我们拒绝了（同时也就接受了备择假设），这表明我们作出了正确的决定。但是，由于假设检验是根据样本提供的信息进行推断的，也就有犯错误的可能。有这样一种情况，原假设正确，而我们却把它当成错误的加以拒绝。犯这种错误的概率用$\alpha$$\alpha$表示，统计上把$\alpha$$\alpha$称为假设检验中的显著性水平 ，也就是决策中所面临的风险。

p-value：p-value是当原假设为真时，比所得到的样本观察结果更极端的结果出现的概率。如果P值很小，说明原假设情况的发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，P值越小，我们拒绝原假设的理由越充分。总之，P值越小，表明结果越显著。但是检验的结果究竟是“显著的”、“中度显著的”还是“高度显著的”，需要我们自己根据P值的大小和实际问题来解决。

案例

抛硬币

问题：给定一枚硬币，通过假设检验确定该硬币是否是均匀的。设$\alpha =5\mathrm{\%}$$\alpha=5\%$

$H_0$$H_0$：该硬币是均匀的

$H_1$$H_1$：该硬币不是均匀的

假设检验过程：连续抛10次硬币，正面朝上10次，反面朝上0次。

在$H_0$$H_0$条件下，即假设硬币是均匀的，那么理论上出现结果【正面朝上10次，反面朝上0次】的概率是$\frac{1}{1024}$$\frac{1}{1024}$。

因为$\frac{1}{1024}<5\mathrm{\%}$$\frac{1}{1024} < 5\%$，因此，拒绝原假设，接受备择假设，即【该硬币不是均匀的】。

均值检验

问题：通过假设检验，判定总体均值是否小于等于85。设$\alpha =5\mathrm{\%}$$\alpha=5\%$

$H_0$$H_0$：$P(\mu \le 85)$$P(\mu \le 85)$

$H_1$$H_1$：$P(\mu >85)$$P(\mu > 85)$

假设检验过程：从总体中抽取10000个样本，计算得到样本均值$\overline{x}=98$$\bar{x}=98$。

根据大数定理，当总体样本数量较大时，可以假设总体样本均值服从高斯分布。如下图所示，$p\mathrm{\_}value=P_r(\overline{x}\ge 98)$$p\_value=P_r(\bar{x} \ge 98)$，而该值小于$\alpha$$\alpha$。因此，拒绝原假设，接受备择假设，即【总体均值大于85】。

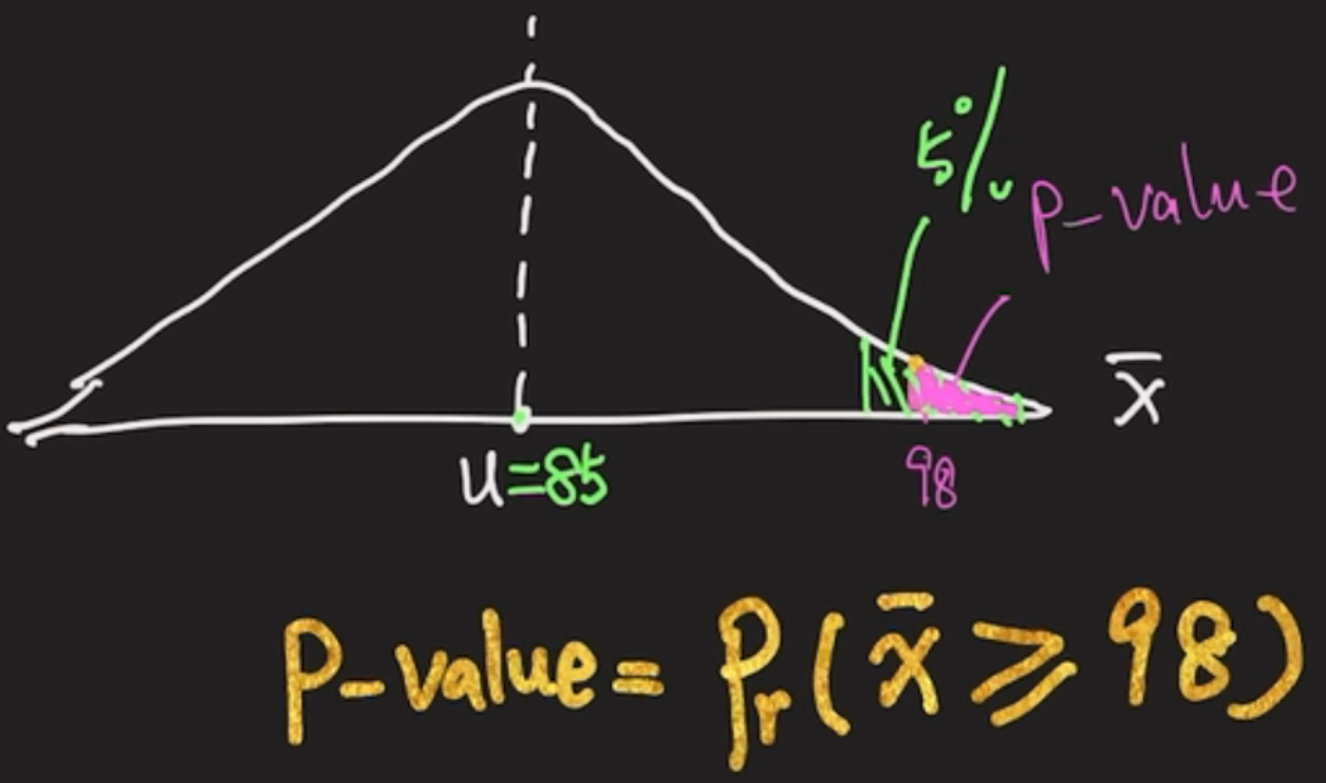
叶老师对p值的解释：The p-value is the probability that you observe the $\overline{x}$$\bar{x}$ greater than the observed value of $\overline{x}$$\bar{x}$（本例中，观察到的$\overline{x}$$\bar{x}$=98）。

参考

1. 统计学｜P-Value｜P值到底是什么｜回答网友提问哔哩哔哩bilibili
2. P值_百度百科 (baidu.com)
3. 显著性水平_百度百科 (baidu.com)