MCMC 2022-10-18
前置知识 PDF:概率密度函数
CDF:累积概率密度函数
示性函数(Indicator function)
(1) I X ( x ) = I { x ∈ X } = { 1 x ∈ X 0 x ∉ X 示性函数有如下性质:示性函数的期望等于下标事件发生的概率
(2) E I { x ∈ X } = 1 ⋅ P { x ∈ X } + 0 ⋅ P { x ∉ X } = P { x ∈ X } 指数分布
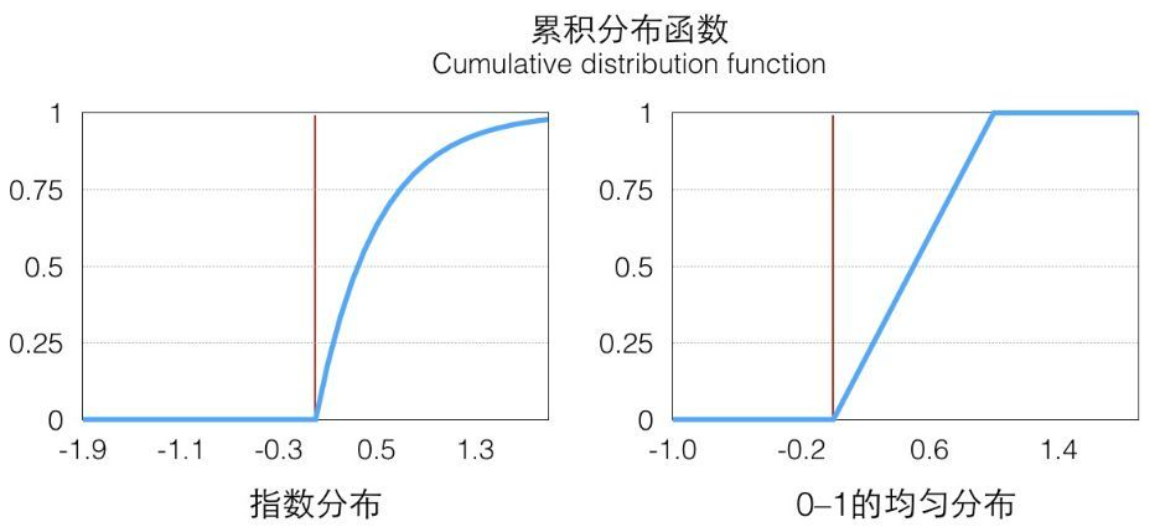
(3) f ( x ) = θ ⋅ e − θ x ( x > 0 ) F ( x ) = 1 − e − θ x ( x > 0 ) 高斯分布
(4) P ( x ) = ϕ ( x ) = 1 2 π ⋅ σ e − ( x − μ ) 2 2 σ 2
MCMC简介 蒙特卡罗法(Monte Carlo method)是通过从概率模型随机抽样然后进行近似数值计算的方法。马尔可夫链蒙特卡罗法(Markov Chain Monte Carlo, MCMC),则是以马尔可夫链为概率模型的蒙特卡罗法。MCMC构建一个马尔可夫链,使其平稳分布就是要进行抽样的分布,首先基于该马尔可夫链进行随机游走,产生样本的序列,之后使用该平稳分布的样本进行近似数值计算。
MCMC包含MH(Metropolis-Hastings)算法和吉布斯抽样算法。
MCMC可用于概率分布的估计、定积分的近似计算、最优化问题求解等问题。
蒙特卡罗法 随机抽样 蒙特卡罗法要解决的问题是:假设概率分布已知,通过抽样获得概率分布的随机样本,然后使用随机样本对概率分布的特征进行分析。例如,通过计算样本均值,从而估计总体期望。
因此,蒙特卡洛法的核心是 随机抽样 。
一般的蒙特卡罗法包括:直接抽样、接受-拒绝抽样、重要性抽样。后两者适合于概率密度函数复杂,不能直接抽样的情况。
直接抽样(逆采样) 对于均匀分布,一般可以使用线性同余发生器生成(0,1)之间的伪随机数。那么,对于其它分布,将其采样转换为(0,1)均匀分布进行采样。转换的方法为:
确定待采样分布的概率密度函数: f ( x ) ,待采样的随机变量为: x
假设(0,1)均匀分布的随机变量为: z
求该概率密度函数的累积概率密度函数: F ( x )
由于 0 ≤ z ≤ 1 , 0 ≤ F ( x ) ≤ 1 ,因此可以定义 z = F ( x ) ,解得: x = G ( z ) 。
所以,通过均匀分布采样得到 z ,带入 G ( z ) 即可得到 x 。
下图以指数分布进行映射示例:
接受-拒绝采样
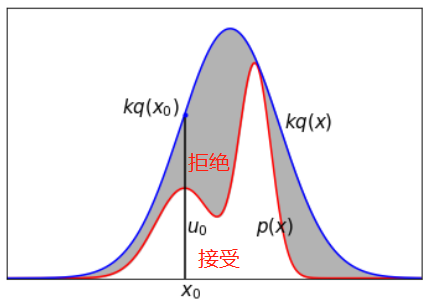
假设 p ( x ) 不可以直接抽样。可以找一个可以直接抽样的分布,称为建议分布。假设 q ( x ) 是建议分布的概率密度函数,并且 k ⋅ q ( x ) > p ( x ) , k > 0 。定义接受-拒绝算法如下:
输入:待抽样概率密度函数 p ( x ) ,满足条件的 k ⋅ q ( x ) ,
输出:随机样本 x 1 , x 2 , ⋯ , x n ,其中, n 为参数
步骤:
从 q ( x ) 中抽样,得到样本 x ∗
从(0,1)均匀分布中抽样,得到 u
如果 u ≤ p ( x ∗ ) k ⋅ q ( x ∗ ) ,则将 x ∗ 作为抽样样本,否则,回到步骤1
直到得到 n 个随机样本,结束。
重要性采样 函数 f ( x ) 在分布 p ( x ) 下的期望也可以写为:
其 中 , 称 为 重 要 性 权 重 (5) E p [ f ( x ) ] = ∫ x f ( x ) p ( x ) d x = ∫ x f ( x ) p ( x ) q ( x ) q ( x ) d x = ∫ x f ( x ) w ( x ) q ( x ) d x = E q [ f ( x ) w ( x ) ] . 其 中 , w ( x ) 称 为 重 要 性 权 重 重要性采样(Importance Sampling)是通过引入重要性权重,将分布 p ( x ) 下 f ( x ) 的期望变为在分布 q ( x ) 下 f ( x ) w ( x ) 的期望,从而可以近似为:
其 中 , 为 独 立 从 中 随 机 抽 取 的 点 (6) f ^ N = 1 N ( f ( x ( 1 ) ) w ( x ( 1 ) ) + ⋯ + f ( x ( N ) ) w ( x ( N ) ) ) 其 中 , x ( 1 ) , x ( 2 ) , ⋯ , x ( N ) 为 独 立 从 q ( x ) 中 随 机 抽 取 的 点 案例: f ( x ) ∼ N ( 0 , 1 ) ,使用采样方法求 P ( X > 8 ) 的概率。
解答:如果直接从 f ( x ) 中采样,只有极少数的点会大于8,因此考虑使用重要性采样法求解。
定义 g ( x ) ∼ N ( 8 , 1 ) ,将目标问题进行如下转换:
(7) P ( X > 8 ) = E f [ I x > 8 ] = ∫ R I x > 8 f ( x ) d x = ∫ R I x > 8 f ( x ) g ( x ) g ( x ) d x = ∫ R I x > 8 1 2 π e − x 2 2 1 2 π e − ( x − 8 ) 2 2 1 2 π e − ( x − 8 ) 2 2 d x = ∫ R I x > 8 e 32 − 8 x 1 2 π e − ( x − 8 ) 2 2 d x 定义 w ( x ) = I x > 8 e 32 − 8 x 。此时,可以将原问题转为函数 w ( x ) 关于概率分布 g ( x ) 期望的问题。接下来,可以从 g ( x ) 中进行采样,得到样本序列 x 1 , x 2 , ⋯ , x N ,将采样点带入 w ( x ) ,可以得到对概率的估计值:
(8) P ( X > 8 ) ≈ 1 N ∑ i = 1 N I x i > 8 e 32 − 8 x i
应用 期望计算 假设有随机变量 x ∈ X ,其概率密度函数为 p ( x ) , f ( x ) 为定义在 X 上的函数,目标是求函数 f ( x ) 关于密度函数 p ( x ) 的数学期望 E p ( x ) [ f ( x ) ] 。针对该问题,蒙特卡罗法通过如下步骤进行解决:
按照概率分布 p ( x ) 独立地抽取 n 个样本 x 1 , x 2 , ⋯ , x n
计算函数 f ( x ) 的样本均值 f ^ n
根据大数定律,当样本容量足够大时,样本均值以概率1收敛于数学期望:
综上述,数学期望的近似值为:
(11) E p ( x ) [ f ( x ) ] ≈ 1 n ∑ n f ( x i )
积分计算 假设有一个函数 h ( x ) ,目标是计算该函数的积分: ∫ X h ( x ) d x
如果将 h ( x ) 分解为一个函数 f ( x ) 和一个概率密度函数 p ( x ) 乘积的形式,那么有:
(12) ∫ X h ( x ) d x = ∫ X f ( x ) p ( x ) d x = E p ( x ) [ f ( x ) ] 因此,函数 h ( x ) 的积分可以表示为函数 f ( x ) 关于概率密度函数 p ( x ) 的期望。而数学期望又可以通过样本均值进行估算。于是,可以通过样本均值近似计算积分,即:
(13) ∫ X h ( x ) d x = E p ( x ) [ f ( x ) ] ≈ 1 n ∑ i = 1 n f ( x i ) 马尔可夫链 基本定义 给定一个随机变量序列 X = { X 0 , X 1 , ⋯ , X t , ⋯ } , X t 表示时刻 t 的随机变量,该随机变量在不同时刻的取值集合相同,即状态空间相同,表示为 S 。随机变量可以是离散的,也可以是连续的。
如果随机变量的状态仅依赖于前一个状态,即:
(14) P ( X t ∣ X 0 , X 1 , ⋯ , X t − 1 ) = P ( X t ∣ X t − 1 ) , t = 1 , 2 , ⋯ 该性质称为 马尔可夫性 。
具有马尔可夫性的随机序列 X = { X 0 , X 1 , ⋯ , X t , ⋯ } 称为马尔可夫链,或马尔科夫过程。条件概率分布 P ( X t ∣ X t − 1 ) 称为马尔可夫链的 转移概率分布 。
若转移概率分布 P ( X t ∣ X t − 1 ) 与 t 无关,即:
(15) P ( X t + s ∣ X t − 1 + s ) = P ( X t ∣ X t − 1 ) , t = 1 , 2 , ⋯ ; s = 1 , 2 , ⋯ 则称该马尔可夫链为时间齐次的马尔可夫链。本文的马尔可夫链都是时间齐次的。
离散状态马尔可夫链 转移概率矩阵和状态分布 若马尔可夫链在时刻 t − 1 处于状态 j ,在时刻 t 移动到状态 i ,将转移概率记作:
其 中 , (16) p i j = P ( X t = i ∣ X t − 1 = j ) , i = 1 , 2 , ⋯ ; j = 1 , 2 , ⋯ 其 中 , p i j ≥ 0 ∑ i p i j = 1 马尔可夫链的转移概率 p i j 可由矩阵表示,即:
其 中 , (17) P = [ p 11 p 12 p 13 ⋯ p 21 p 22 p 23 ⋯ p 31 p 32 p 33 ⋯ ⋯ ⋯ ⋯ ⋯ ] 其 中 , p i j ≥ 0 ∑ i p i j = 1 考虑马尔可夫链 X = { X 0 , X 1 , ⋯ , X t , ⋯ } 在时刻 t ( t = 0 , 1 , 2 , ⋯ ) 的概率分布,称为时刻 t 的 状态分布 ,记作:
其 中 , 表 示 时 刻 状 态 为 的 概 率 (18) π ( t ) = [ π 1 ( t ) π 2 ( t ) ⋮ ] 其 中 , π i ( t ) 表 示 时 刻 t 状 态 为 i 的 概 率 P ( X t = i ) 对于初始分布 π ( 0 ) ,其向量通常只有一个分量为1,其余为0,表示马尔可夫链从一个具体状态开始。
马尔可夫链 X 在时刻 t 的状态分布,可以由时刻 t − 1 的状态分布以及转移概率分布决定:
这是因为(对时刻 t 状态为 i 进行推导,其余状态类似):
(20) π i ( t ) = P ( X t = i ) = ∑ j P ( X t = i ∣ X t − 1 = j ) P ( X t − 1 = j ) = ∑ j p i j π j ( t − 1 ) 假设有三个状态,那么转移公式为:
(21) [ p 11 p 12 p 13 p 21 p 22 p 23 p 31 p 32 p 33 ] [ π 1 ( t − 1 ) π 2 ( t − 1 ) π 3 ( t − 1 ) ] = [ π 1 ( t ) π 2 ( t ) π 3 ( t ) ] 马尔可夫链在时刻 t 的状态分布,可以通过递推得到。由上述公式:
(22) π ( t ) = P π ( t − 1 ) = P ( P π ( t − 2 ) ) = P 2 π ( t − 2 ) 通过递推得到:
其中, P t 称为 t 步转移概率矩阵,表示时刻 0 从状态 j 出发,时刻 t 到达状态 i 的 t 步转移概率:
平稳分布 对马尔可夫链 X = { X 0 , X 1 , ⋯ , X t , ⋯ } ,其状态空间为 S ,转移概率矩阵为 P = ( p i j ) ,如果存在状态空间 S 上的一个分布:
使得:
则称 π 为马尔可夫链 X = { X 0 , X 1 , ⋯ , X t , ⋯ } 的平稳分布。
直观上,如果马尔可夫链的平稳分布存在,那么以该分布为初始分布,然后进行随机状态转移,之后任何一个时刻的状态分布都是平稳分布。
连续状态马尔可夫链 将离散状态马尔可夫链中的转移概率矩阵替换为转移核,其它概率类似,不再赘述。
马尔可夫链性质 不可约
从任意状态出发,当经过充分长时间后,可以到达任意状态。
非周期
不存在一个状态,从该状态出发,再返回该状态,经历的时间呈周期性。
正常返
对其中任意一个状态,从其它任意一个状态出发,当时间趋于无穷时,首次转移到这个状态的概率不为0。
遍历定理
如果马尔可夫链是不可约、非周期且正常返的,则该马尔可夫链有唯一平稳分布。
满足相应条件的马尔可夫链,当时间趋于无穷时,其状态分布接近于平稳分布。(注:可以理解为首先初始化一个状态分布,然后通过无数次迭代转移,最后状态分布趋于平稳分布)。
可逆马尔可夫链
如果对马尔可夫链,满足:
(27) π j ⋅ P ( X t = i ∣ X t − 1 = j ) = π i ⋅ P ( X t − 1 = j ∣ X t = i ) , i , j = 1 , 2 , ⋯ 或者简写为(此式称为细致平衡方程):
则称该马尔可夫链为可逆的马尔可夫链。
(定理)满足细致平衡方程的状态分布 π ,就是该马尔可夫链的平稳分布,即 P π = π ,证明如下:
(29) P π i = ∑ j p i j π j = ∑ j p j i π i = π i ∑ j p j i = π i , i = 1 , 2 , ⋯ 马尔可夫链蒙特卡罗法 基本步骤 马尔可夫链蒙特卡罗法的基本步骤如下:
在随机变量 x 的状态空间 S 上构造一个满足遍历定理的马尔可夫链,使其平稳分布为目标分布 p ( x )
从状态空间的某一点 x 0 出发,用构造的马尔可夫链进行随机游走,产生样本序列 x 0 , x 1 , x 2 , ⋯ , x t , ⋯
应用马尔可夫链的遍历定理,确定正整数 m 和 n , m < n ,前 m 个样本处于燃烧期,被丢弃掉。得到样本集合 x m + 1 , x m + 2 , ⋯ , x n ,求得函数 f ( x ) 的均值(遍历均值)
需要考虑的几个重要问题:
如何定义马尔可夫链,保证马尔可夫链蒙特卡罗法的条件成立; 如何确定收敛步数 m ,保证样本抽取的无偏性; 如何确定迭代步数 n ,保证遍历均值计算的精度。
Metropolis-Hastings 算法 马尔可夫链 假设要抽样的概率分布为 p ( x ) ,M-H算法采用转移核为 p ( x , x ′ ) 的马尔可夫链:
其 中 , 为 建 议 分 布 为 接 受 分 布 (31) p ( x , x ′ ) = q ( x , x ′ ) α ( x , x ′ ) 其 中 , q ( x , x ′ ) 为 建 议 分 布 α ( x , x ′ ) 为 接 受 分 布 建议分布 q ( x , x ′ ) 为另一个马尔可夫链的转移核,并且是不可约的,同时是一个容易抽样的分布。
接受分布 α ( x , x ′ ) 定义如下:
(32) α ( x , x ′ ) = min { 1 , p ( x ′ ) q ( x ′ , x ) p ( x ) q ( x , x ′ ) } 那么,转移核 p ( x , x ′ ) 可以写为:
(33) p ( x , x ′ ) = { q ( x , x ′ ) , p ( x ′ ) q ( x ′ , x ) ⩾ p ( x ) q ( x , x ′ ) q ( x ′ , x ) p ( x ′ ) p ( x ) , p ( x ′ ) q ( x ′ , x ) < p ( x ) q ( x , x ′ ) 转移核为 p ( x , x ′ ) 的马尔可夫链上的随机游走以如下方式进行:
假设时刻 t − 1 状态为 x ,即 x t − 1 = x
按建议分布 q ( x , x ′ ) 抽样产生一个候选状态 x ′
按照接受分布 α ( x , x ′ ) 抽样决定是否接受 x ′ :接受概率为 α ( x , x ′ ) ,拒绝概率为 1 − α ( x , x ′ ) 。具体地,从区间(0,1)上均匀分布抽取一个随机数 u ,决定时刻 t 的状态:
(34) x t = { x ′ , u ⩽ α ( x , x ′ ) x , u > α ( x , x ′ ) 如果接受,则时刻 t 转移到 x ′ ,否则,仍停留在状态 x
可以证明,转移核为 p ( x , x ′ ) 的马尔可夫链是可逆马尔可夫链(满足遍历定理),其平稳分布就是 p ( x ) ,即要抽样的目标分布。
证明过程:
如果 x = x ′ ,显然 p ( x ) p ( x , x ′ ) = p ( x ′ ) p ( x ′ , x ) 成立
如果 x ≠ x ′ ,则
(35) p ( x ) p ( x , x ′ ) = p ( x ) q ( x , x ′ ) min { 1 , p ( x ′ ) q ( x ′ , x ) p ( x ) q ( x , x ′ ) } = min { p ( x ) q ( x , x ′ ) , p ( x ′ ) q ( x ′ , x ) } = p ( x ′ ) q ( x ′ , x ) min { p ( x ) q ( x , x ′ ) p ( x ′ ) q ( x ′ , x ) , 1 } = p ( x ′ ) q ( x ′ , x ) α ( x ′ , x ) = p ( x ′ ) p ( x ′ , x ) 因此, p ( x ) p ( x , x ′ ) = p ( x ′ ) p ( x ′ , x ) 也成立,该马尔可夫链为可逆马尔可夫链。
由 p ( x ) p ( x , x ′ ) = p ( x ′ ) p ( x ′ , x ) 可知:
(36) ∫ p ( x ) p ( x , x ′ ) d x = ∫ p ( x ′ ) p ( x ′ , x ) d x = p ( x ′ ) ∫ p ( x ′ , x ) d x = p ( x ′ ) 根据平稳分布的定义, p ( x ) 是马尔可夫链的平稳分布。
建议分布 建议分布 q ( x , x ′ ) 有多种可能的形式,以下介绍常用的两种。
对称式
假设建议分布是对称的,即对任意的 x 和 x ′ ,有:
如果选择该分布,也可称为Metropolis算法。此时,接受分布 α ( x , x ′ ) 可以简化为:
(38) α ( x , x ′ ) = min { 1 , p ( x ′ ) p ( x ) } Metropolis选择的一个特例是 q ( x , x ′ ) 取条件概率分布 p ( x ′ ∣ x ) ,定义为多元正态分布,其均值为 x ,其协方差矩阵是常数矩阵。
Metropolis选择的特点是当 x ′ 与 x 接近时, q ( x , x ′ ) 的概率值高,否则 q ( x , x ′ ) 的概率值低。 状态转移在附近点的可能性更大 。
独立抽样
假设 q ( x , x ′ ) 与当前状态 x 无关,即 q ( x , x ′ ) = q ( x ′ ) ,建议分布的计算按照 q ( x ′ ) 独立抽样进行。
独立抽样实现简单,但是收敛速度可能较慢,通常选择接近目标分布 p ( x ) 的分布作为建议分布 q ( x ) 。
满条件分布 马尔可夫链蒙特卡罗法的目标分布通常是多元联合概率分布 , 其 中 p ( x ) = p ( x 1 , x 2 , ⋯ , x k ) , 其 中 x = ( x 1 , x 2 , ⋯ , x k ) T 为 k 维随机变量。如果条件概率分布 p ( x I ∣ x − I ) 中所有 k 个变量都出现,其中 x I = { x i , i ∈ I } , x − I = { x i , i ∉ I } , I ⊂ K = { 1 , 2 , ⋯ , k } ,那么这种条件概率分布为满条件概率分布。
满条件概率分布有以下性质,对任意的 x , x ′ ∈ X 和任意的 I ⊂ K ,有:
(39) p ( x I ∣ x − I ) = p ( x ) ∫ p ( x ) d x I ∝ p ( x ) p ( x I ′ ∣ x − I ′ ) p ( x I ∣ x − I ) = p ( x ′ ) p ( x ) 在MH算法中,可以利用该性质简化计算,提高计算效率。具体地, p ( x I ′ ∣ x − I ′ ) p ( x I ∣ x − I ) 比 p ( x ′ ) p ( x ) 更容易计算。
MH算法步骤 输入:待抽样的目标分布 p ( x ) ,函数 f ( x ) ,建议分布 q ( x )
输出: p ( x ) 的随机样本 x m + 1 , x m + 2 , ⋯ , x n ,函数样本均值 f m n
参数:收敛步数 m ,迭代步数 n
步骤:
任意选择一个初始值 x 0
对 i = 1 , 2 , ⋯ , n 循环执行
a) 设状态 x i − 1 = x ,按照建议分布 q ( x , x ′ ) 随机抽取一个候选状态 x ′
b) 计算接受概率
(40) α ( x , x ′ ) = min { 1 , p ( x ′ ) q ( x ′ , x ) p ( x ) q ( x , x ′ ) } c) 从区间(0,1)中按均匀分布随机抽取一个数 u
如 u ≤ α ( x , x ′ ) ,则状态 x i = x ′ ,否则,状态 x i = x
得到样本集合 x m + 1 , x m + 2 , ⋯ , x n ,计算
吉布斯抽样 基本原理 吉布斯抽样是MH算法的特殊情况,多用于多元变量联合分布的抽样和估计。其基本做法是,从联合概率分布定义满条件概率分布,依次对满条件概率分布进行抽样,得到样本的序列。
假设多元变量的联合概率分布为 p ( x ) = p ( x 1 , x 2 , ⋯ , x k ) 。吉布斯抽样从一个初始样本 x ( 0 ) = ( x 1 ( 0 ) , x 2 ( 0 ) , ⋯ , x k ( 0 ) ) T 出发,不断迭代,每次迭代得到联合分布的一个样本 x ( i ) = ( x 1 ( i ) , x 2 ( i ) , ⋯ , x k ( i ) ) T 。最终,得到抽样样本序列 x ( 0 ) , x ( 1 ) , ⋯ , x ( n ) 。
在每次迭代中,依次对 k 个随机变量中的一个变量进行抽样。例如,在第 i 次迭代中,对第 j 个变量进行随机抽样,那么抽样的分布是满条件概率分布 p ( x j ∣ x − j ( i ) ) 。
假设在第 i − 1 步得到样本 ( x 1 ( i − 1 ) , x 2 ( i − 1 ) , ⋯ , x k ( i − 1 ) ) T ,在第 i 步,首先对第一个变量按照以下满条件概率分布随机抽样:
(42) x 1 ( i ) ← p ( x 1 ∣ x 2 ( i − 1 ) , x 3 ( i − 1 ) , ⋯ , x k ( i − 1 ) ) x 2 ( i ) ← p ( x 2 ∣ x 1 ( i ) , x 3 ( i − 1 ) , ⋯ , x k ( i − 1 ) ) x 3 ( i ) ← p ( x 3 ∣ x 1 ( i ) , x 2 ( i ) , x 4 ( i − 1 ) , ⋯ x k ( i − 1 ) ) ⋮ x j ( i ) ← p ( x j ∣ x 1 ( i ) , ⋯ , x j − 1 ( i ) , x j + 1 ( i − 1 ) , ⋯ , x k ( i − 1 ) ) ⋮ x k ( i ) ← p ( x k ∣ x 1 ( i ) , x 2 ( i ) , ⋯ , x k − 1 ( i ) ) 于是得到第 i 步的整体样本 x ( i ) = ( x 1 ( i ) , x 2 ( i ) , ⋯ , x k ( i ) ) T 。
吉布斯抽样是单分量MH算法的特殊情况。定义建议分布是当前变量 x j ( j = 1 , 2 , ⋯ , k ) 的满条件概率分布:
这时,接受概率 α = 1 :
(44) α ( x , x ′ ) = min { 1 , p ( x ′ ) q ( x ′ , x ) p ( x ) q ( x , x ′ ) } = min { 1 , p ( x ′ − j ) p ( x ′ j ∣ x ′ − j ) p ( x j ∣ x ′ − j ) p ( x − j ) p ( x j ∣ x − j ) p ( x ′ j ∣ x − j ) } = 1 这里用到 p ( x − j ) = p ( x ′ − j ) 和 p ( ⋅ ∣ x − j ) = p ( ⋅ ∣ x ′ − j )
转移核就是满条件概率分布:
吉布斯抽样对每次抽样的结果都接受,没有拒绝,这一点和一般的MH算法不同。
这里,假设满条件概率分布 p ( x j ′ ∣ x − j ) 不为0,即马尔可夫链是不可约的。
吉布斯抽样算法步骤 输入:目标概率分布的密度函数 p ( x ) ,函数 f ( x )
输出: p ( x ) 的随机样本 x m + 1 , x m + 2 , ⋯ , x n ,函数样本均值 f m n
参数:收敛步数m,迭代步数n
步骤:
(1) 初始化样本 x ( 0 ) = ( x 1 ( 0 ) , x 2 ( 0 ) , ⋯ , x k ( 0 ) ) T
(2) 对步数 i 进行循环
设第 i − 1 次迭代的样本为 x ( i − 1 ) = ( x 1 ( i − 1 ) , x 2 ( i − 1 ) , ⋯ , x k ( i − 1 ) ) T ,则第 i 次迭代进行如下几步操作:
(1) 由满条件概率分布 p ( x 1 ∣ x 2 ( i − 1 ) , ⋯ , x k ( i − 1 ) ) 抽取 x 1 ( i )
⋮
(j) 由满条件概率分布 p ( x j ∣ x 1 ( i ) , ⋯ , x j − 1 ( i ) , x j + 1 ( i − 1 ) , ⋯ , x k ( i − 1 ) ) 抽取 x j ( i )
⋮
(k) 由满条件概率分布 p ( x k ∣ x 1 ( i ) , ⋯ , x k − 1 ( i ) ) 抽取 x k ( i )
得到第 i 次迭代值 x ( i ) = ( x 1 ( i ) , x 2 ( i ) , ⋯ , x k ( i ) ) T
(3) 得到样本集合
(46) { x ( m + 1 ) , x ( m + 2 ) , ⋯ , x ( n ) } (4) 计算
(47) f m n = 1 n − m ∑ i = m + 1 n f ( x ( i ) ) 吉布斯抽样示例 假设要采样的是二维正态分布 N ( μ , Σ ) ,其中:
(48) μ = ( μ 1 , μ 2 ) = ( 5 , − 1 ) Σ = ( σ 1 2 ρ σ 1 σ 2 ρ σ 1 σ 2 σ 2 2 ) = ( 1 1 1 4 ) ρ = 0.5 首先,需要求状态转移满条件分布:
(49) P ( x 1 ∣ x 2 ) = N ( μ 1 + ρ σ 1 / σ 2 ( x 2 − μ 2 ) , ( 1 − ρ 2 ) σ 1 2 ) P ( x 2 ∣ x 1 ) = N ( μ 2 + ρ σ 2 / σ 1 ( x 1 − μ 1 ) , ( 1 − ρ 2 ) σ 2 2 ) 证明:已知
(50) f ( x 1 , x 2 ) = 1 2 π σ 1 σ 2 1 − ρ 2 exp { − 1 2 ( 1 − ρ 2 ) [ ( x 1 − μ 1 σ 1 ) 2 − 2 ρ ( x 1 − μ 1 σ 1 ) ( x 2 − μ 2 σ 2 ) + ( x 2 − μ 2 σ 2 ) 2 ] } f ( x 2 ) = 1 2 π σ 2 exp { − ( x 2 − μ 2 ) 2 2 σ 2 2 } 因此:
(51) f ( x 1 ∣ x 2 ) = 1 2 π σ 1 1 − ρ 2 exp { − 1 2 ( 1 − ρ 2 ) σ 1 2 [ x 1 − μ 1 − σ 1 σ 2 ρ ( x 2 − μ 2 ) ] 2 } 确定了目标分布的满条件分布,接下来可以使用吉布斯抽样得到样本:
采样一个初始状态: ( x 1 ( 0 ) , x 2 ( 0 ) ) ,设燃烧期样本数为 m ,需要得到的样本数为 n
for i in range(1, m+n):
x 1 ( i ) ∼ P ( x 1 ∣ x 2 ( i − 1 ) )
x 2 ( i ) ∼ P ( x 2 ∣ x 1 ( i − 1 ) )
得到样本集合 { ( x 1 ( m + 1 ) , x 2 ( m + 1 ) ) , ( x 1 ( m + 2 ) , x 2 ( m + 2 ) ) , … , ( x 1 ( m + n ) , x 2 ( m + n ) ) }
参考文档 李航 《统计学习方法》 第十九课 马尔可夫链蒙特卡罗法 (julyedu.com) 蒙特卡罗算法 - 知乎 (zhihu.com) (1 封私信 / 62 条消息) 如何理解蒙特卡洛方法的接受拒绝采样? - 知乎 (zhihu.com) 使用蒙特卡洛计算定积分(附Python代码) - Ji-Huan Guan (guanjihuan.com) (145条消息) MCMC 方法与示例 禾雨辰子的博客-CSDN博客_mcmc方法 你一定从未看过如此通俗易懂的马尔科夫链蒙特卡罗方法(MCMC)解读(上) - 知乎 (zhihu.com) 你一定从未看过如此通俗易懂的马尔科夫链蒙特卡罗方法(MCMC)解读(下) - 知乎 (zhihu.com) (144条消息) python实现Metropolis采样算法实例_David-Chow的博客-CSDN博客 Monte Carlo笔记-2:MCMC,附简易python代码 - simplex - 博客园 (cnblogs.com) 用Python实现马尔可夫链蒙特卡罗 - 知乎 (zhihu.com) 如何快速理解马尔科夫链蒙特卡洛法? - 知乎 (zhihu.com) 机器学习中的数学-07讲-常见的采样方法4 (重要性采样1) 哔哩哔哩 bilibili Markov Chain Monte Carlo (MCMC) — Computational Statistics in Python 0.1 documentation (duke.edu)