从DT到GBDT2022-01-06

算法架构

模型架构

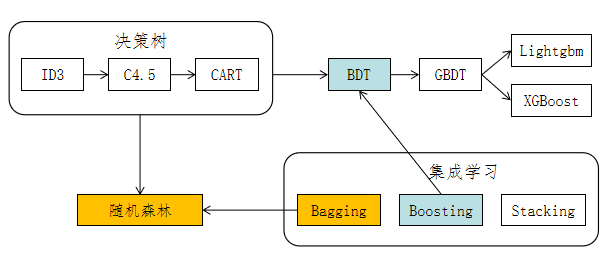
名词解释：

DT：decision tree，决策树
BDT：boosting decision tree，集成决策树
GBDT：gradient boosting decision tree，梯度提升决策树

预备知识

信息量

对某个事件发生概率的度量。一般情况下，概率越低，则事件包含的信息量越大。衡量事件信息量的公式如下：

\begin{matrix} (1) & I = l o g \frac{1}{p} = - l o g p \end{matrix}

熵（Entropy）

熵是随机变量不确定性的度量。

设X是一个取值个数为n的离散随机变量，其概率分布为：

\begin{matrix} (2) & P (X = x_{i}) = p_{i}, i = 1, 2, . . ., n \end{matrix}

则随机变量X的熵定义为：

\begin{matrix} (3) & H (X) = - \sum_{i = 1}^{n} p_{i} * l o g p_{i} \end{matrix}

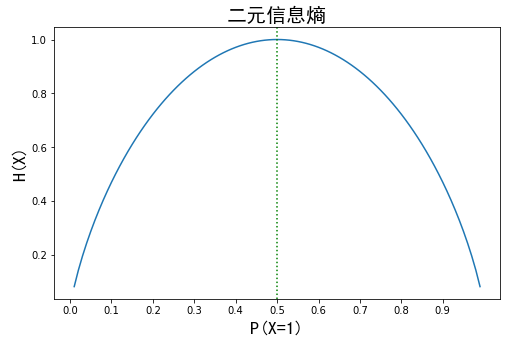
熵越大，随机变量取值的不确定性越大，反之越小。当随机变量的分布为均匀分布时，该随机变量的熵最大。下图为二分类时熵与概率的变化曲线，可以看出，当P(X=1)=0.5时，H(X)最大。

二元信息熵

条件熵

表示在已知随机变量X的条件下随机变量Y的不确定性。

设随机变量（X,Y），其联合概率分布为：

\begin{matrix} (4) & P (X, Y) = p_{i j} (i = 1, 2, . . ., n; j = 1, 2, . . ., m) \end{matrix}

给定随机变量X的条件下随机变量Y的条件熵为H(Y|X)，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：

\begin{matrix} (5) & \begin{matrix} H (Y | X) = \sum p_{i} * H (Y | X = x_{i}) \\ p_{i} = P (X = x_{i}), i = 1, 2, 3, . . ., n \end{matrix} \end{matrix}

信息增益

表示得知特征X的信息从而使得类Y的信息的不确定性减少的程度。

$g(D,A)$ ，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即

\begin{matrix} (6) & g (D, A) = H (D) - H (D | A) \end{matrix}

$g(D,A)$ 越大，反之越小。

信息增益比

$g_R(D,A)$ 信息增益 $g(D, A)$ 训练数据集D关于特征A的值的熵 $H_A(D)$ 之比，即：

\begin{matrix} (7) & g_{R} (D, A) = \frac{g (D, A)}{H_{A} (D)} \end{matrix}

\begin{matrix} (8) & 其 中 ， H_{A} (D) = - \sum_{i = 1}^{n} \frac{| D_{i} |}{| D |} l o g_{2} \frac{| D_{i} |}{| D |} ， n 是 特 征 A 取 值 的 个 数 \end{matrix}

$g_R(D,A)$ 越小，反之越大。

基尼指数

$p_k$ ，则概率分布的基尼指数定义为：

\begin{matrix} (9) & G i n i (p) = \sum_{k = 1}^{K} p_{k} (1 - p_{k}) = 1 - \sum_{k = 1}^{K} p_{k}^{2} \end{matrix}

对于给定的样本集合D，其基尼指数为：

\begin{matrix} (10) & \begin{matrix} G i n i (D) = 1 - \sum_{k = 1}^{K} {(\frac{| C_{k} |}{| D |})}^{2} \\ 其 中 ， C_{k} 是 D 中 属 于 第 k 类 的 样 本 子 集 ， K 是 类 的 个 数 \end{matrix} \end{matrix}

如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，即：

\begin{matrix} (11) & \begin{matrix} D 1 = {(x, y) \in D | A (x) = a} \\ D 2 = D - D 1 \end{matrix} \end{matrix}

则在特征A是否取a的条件下，集合D的基尼指数定义为：

\begin{matrix} (12) & G i n i (D, A) = \frac{| D 1 |}{| D |} G i n i (D_{1}) + \frac{| D 2 |}{| D |} G i n i (D_{2}) \end{matrix}

Gini(D)表示集合D的不确定性，Gini(D,A)表示将A=a分割后集合D的不确定性。

基尼指数越大，样本集合的不确定性（不纯度）越大，与熵类似。

下式表明基尼指数为熵的一阶泰勒近似值：

\begin{matrix} (13) & \begin{aligned} 将 f (x) & = - l n x 在 x = 1 处 进 行 一 阶 泰 勒 展 开 ： \\ f (x) & = f (x_{0}) + f^{^{'}} (x - x_{0}) + o (\cdot) \\ = f (1) + f^{^{'}} (1) (x - 1) + o (\cdot) \\ \approx 1 - x \end{aligned} \end{matrix}

\begin{matrix} 因 此 ， 随 机 变 量 X 的 熵 近 似 于 其 概 率 分 布 的 基 尼 指 数 : \\ \begin{matrix} (14) & \begin{aligned} H (X) & = \sum_{i = 1}^{n} p_{i} * (- l o g p_{i}) \\ \approx \sum_{i = 1}^{n} p_{i} * (1 - p_{i}) \\ = G i n i (p) \end{aligned} \end{matrix} \end{matrix}

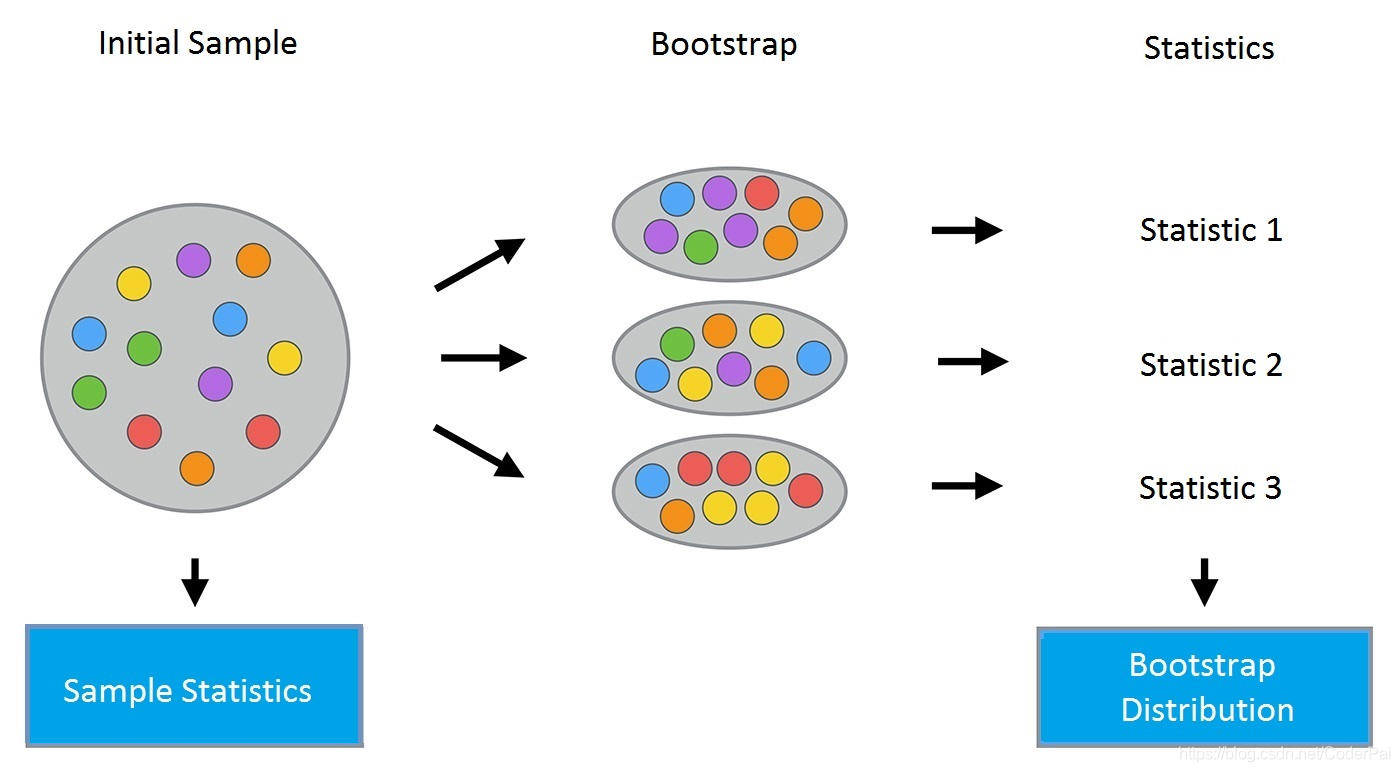
自助法

自助法(bootstrapping)是一种数据采样方法，过程如下：

$D$ $D$ $D^{'}$ $D^{'}$ $D^{'}$ $D^{'}$ $D-D^{'}$ 用作测试集。

将上述过程重复N次，便可以得到N个采样后的样本集。

bootstrapping

Bias-Variance Trade-off

符号	含义
$x$	测试样本
$D$	数据集
$y$	$x$ 的真实标记
$y_D$	$x$ 在数据集中的标记
$f(x;D)$	$D$ $f$ $x$ 上的预测输出
$\bar{f}(x)$	$f(x;D)$ $x$ 的期望预测输出
$\varepsilon$	$y-y_D$

符号图形化展示如下：

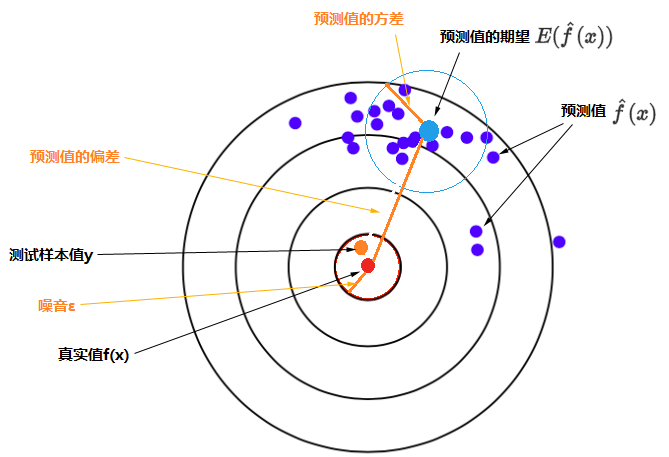
bias_and_variance_desc

期望预测输出
$\begin{matrix} (15) & \bar{f} (x) = E [f (x; D)] \end{matrix}$
噪声
$\varepsilon$ 的期望为0，所以：

\begin{matrix} (16) & \begin{aligned} E (ε) & = E (y - y_{D}) = 0 \\ V a r (ε & ) = V a r (y - y_{D})^{2} \\ = E (y - y_{D})^{2} - {(E (y - y_{D}))}^{2} \\ = E (y - y_{D})^{2} \end{aligned} \end{matrix}

噪声用于刻画学习问题本身的难度。

方差
使用样本数相同不同训练集 $x$ 预测输出值之间的差异程度：

\begin{matrix} (17) & V a r (x) = E [(f (x; D) - \bar{f})^{2}] \end{matrix}

$x$ 的预测结果的离散程度。

偏差
期望输出（所有可能的训练数据集训练出的所有模型的输出的平均值）与真实标记的差别称为偏差（bias），即：

\begin{matrix} (18) & b i a s^{2} (x) = (\bar{f} - y)^{2} \end{matrix}

偏差用于刻画学习算法本身的拟合能力。

期望泛化误差

\begin{matrix} (19) & \begin{aligned} E (f; D) & = E [(f (x; D) - y_{D})^{2}] \\ = E [(f (x; D) - \bar{f} + \bar{f} - y_{D})^{2}] \\ = E [(f (x; D) - \bar{f})^{2}] + E [(\bar{f} - y_{D})^{2}] + 2 * E [(f (x; D) - \bar{f}) * (\bar{f} - y_{D})] \\ = V a r (x) + E [(\bar{f} - y + y - y_{D})^{2}] \\ = V a r (x) + E [(\bar{f} - y)^{2}] + E [(y - y_{D})^{2}] + 2 * E [(\bar{f} - y) (y - y_{D})] \\ = V a r (x) + (\bar{f} - y)^{2} + V a r (ε) \\ = V a r (x) + b i a s^{2} (x) + V a r (ε) \end{aligned} \end{matrix}

偏差-方差分解说明，泛华性能由学习算法的能力、数据的充分性以及学习任务本身的难度共同决定。

直观展示
下图将机器学习任务描述为一个「打靶」的活动：根据相同算法、不同数据集训练出的模型，对同一个样本进行预测；每个模型作出的预测相当于是一次打靶。
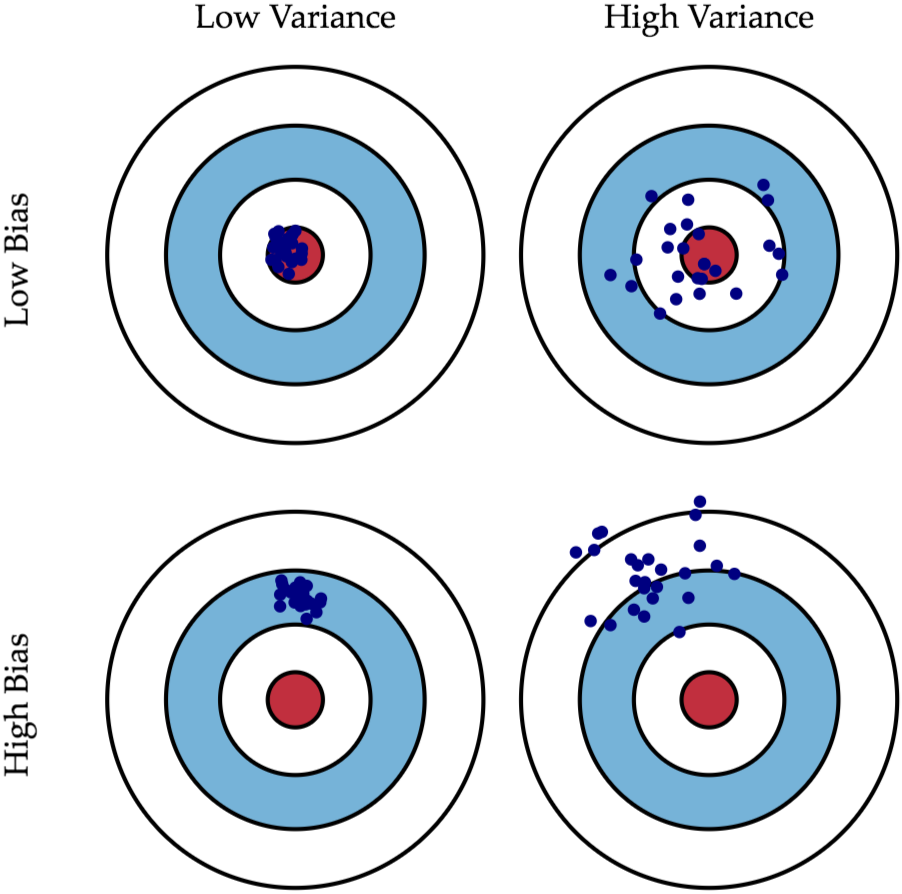
- 左上角：低偏差，低方差。如果有无穷的训练数据，以及完美的模型算法，有希望达成这样的情况。然而，现实中的工程问题，通常数据量是有限的，而模型也是不完美的。因此，这只是一个理想状况。
- 右上角：低偏差，高方差。靶纸上的落点都集中分布在红心周围，它们的期望落在红心之内，因此偏差较小。另外一方面，落点虽然集中在红心周围，但是比较分散，这是方差大的表现。
- 左下角：高偏差，低方差。靶纸上的落点非常集中，说明方差小。但是落点集中的位置距离红心很远，这是偏差大的表现。
- 右下角：高偏差，高方差。最差的情况。
总结
- 泛化误差由偏差、方差、噪声构成。
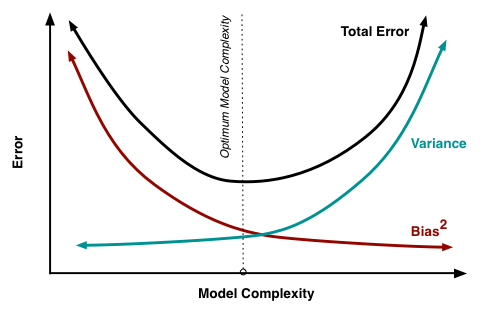
- 模型训练的起始阶段，拟合效果差，偏差较大，数据集的变化对于模型的影响也很小，因此方差较小。此时模型表现为欠拟合。
- 随着训练得深入，模型的拟合能力越来越强，偏差逐渐减小，方差逐渐增大。
- 当模型训练到一定程度时，它的拟合能力非常强，这时所有样本都可以很好地被拟合，偏差很小，但是训练集细微的变化都会对模型的效果产生很大的影响，方差很大，将发生过拟合。

bias_variance_tradeoff

决策树

概述

决策树是一种基本的分类与回归方法，它可以认为是一种if-then规则的集合。决策树由节点和有向边组成，内部节点代表特征，叶子节点代表类别。

下图为决策树的一个图例，判断用户是否有贷款意向：

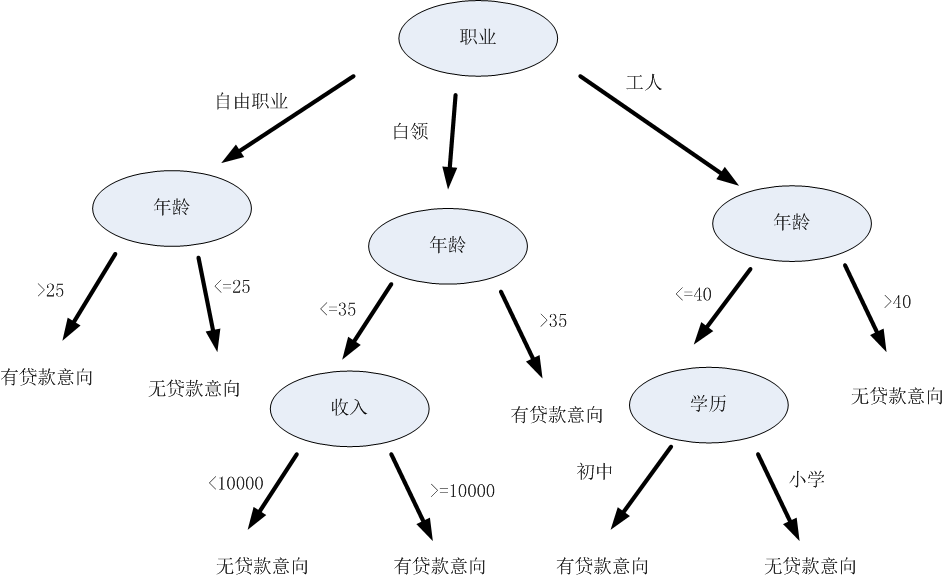
决策树示例

决策树递归地选择特征并对整个特征空间进行划分，从而对样本进行分类，其过程如下所示：

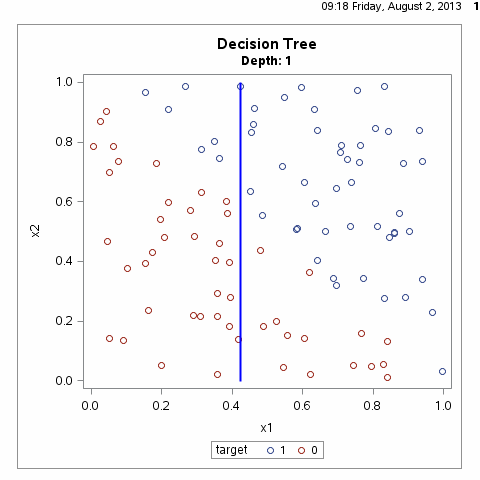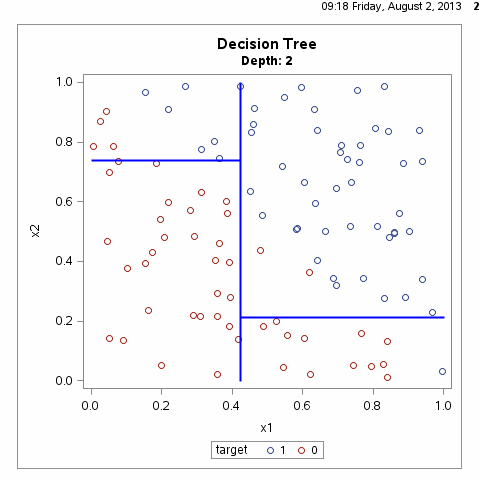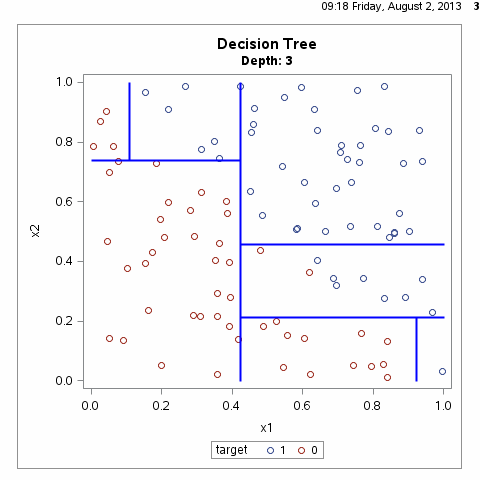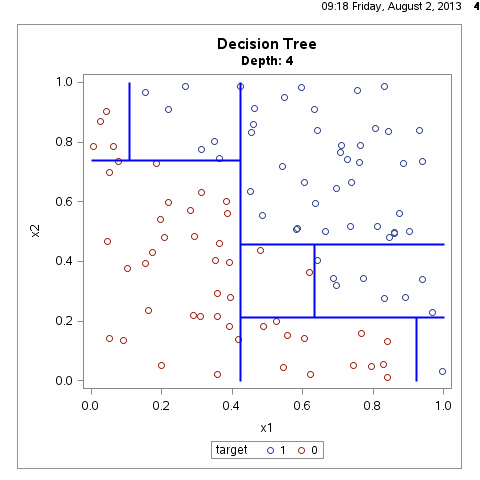
决策树生成过程

从上图可以看出，决策树划分的方式有无数种，如何得到最优的决策树？即对训练数据有较好分类效果，同时对测试数据有较低的误差率。

根据特征选择依据的不同，决策树有三种生成算法，包括：ID3、C4.5、CART(Classification and Regression Tree)。

ID3

一、特征选择依据：选择信息增益最大的特征。

二、构建过程：

$\varepsilon$

输出：决策树T

主要过程：

$A_g$ ；

$A_g$ $\varepsilon$ $C_k$ 作为该节点的类标记，返回T；

$A_g$ $a_i$ $A_g=a_i$ $D_i$ $D_i$ 中实例数最大的类作为标记，构建子节点，由节点及其子节点构成树T，返回T；

$D_i$ $A-\{A_g\}$ $T_i$ $T_i$ 。

三、优点

1、构建决策树的速度比较快，算法实现简单，生成的规则容易理解。

四、缺点

1、倾向选择取值较多的特征。

2、只能处理离散特征，不能处理连续特征。

3、无修剪过程。

C4.5

一、特征选择依据：选择信息增益比最大的特征。

二、构建过程

$\varepsilon$

输出：决策树T

主要过程：

$g_R(D, A)$ $A_g$ ；

$A_g$ $\varepsilon$ $C_k$ 作为该节点的类标记，返回T；

$A_g$ $a_i$ $A_g=a_i$ $D_i$ $D_i$ 中实例数最大的类作为标记，构建子节点，由节点及其子节点构成树T，返回T；

$D_i$ $A-\{A_g\}$ $T_i$ $T_i$ 。

三、优点

1、能够处理缺失值

a、计算信息增益比时缺失：忽略；将此属性出现频率最高的值赋予该样本。

b、按该属性创建分支时缺失：忽略；将此属性出行频率最高的值赋予该样本；为缺失值创建一个分支。

c、预测时，待分类样本的属性缺失：到达该属性时结束，将该属性所对应子树中概率最大的类别作为预

测类别；将此属性出行频率最高的值赋予该样本，然后继续预测。

2、能够处理离散值和连续值（按属性值排序，按二分法枚举两两属性值之间的阈值点进行离散化）。

3、构造树有后有剪枝操作，防止过拟合。

四、缺点

1、倾向选择取值较少的特征。

2、针对连续值特征，计算效率低。

CART

一、特征选择依据：选择基尼指数最小的特征。

二、构建过程 - 回归树

输入：训练数据集D

输出：回归树f(x)

主要过程：

$j$ $j$ $s$ $(j, s)$

\begin{matrix} (20) & \underset{j, s}{m i n} [\underset{c_{1}}{m i n} \sum_{x_{i} \in R_{1} (j, s))} (y_{i} - c_{1})^{2} + \underset{c_{1}}{m i n} \sum_{x_{i} \in R_{2} (j, s))} (y_{i} - c_{2})^{2}] \end{matrix}

$(j,s)$ 划分区域并决定相应的输出值：

\begin{matrix} (21) & \begin{matrix} R_{1} (j, s) = {x | x^{(j)} ⩽ s} \\ R_{2} (j, s) = {x | x^{(j)} > s} \\ {\hat{c}}_{m} = \frac{1}{N_{m}} \sum_{x_{i} \in R_{m} (j, s)} y_{i}, x \in R_{m}, m = 1, 2, N_{m} 为 R_{m} 元 素 个 数 \end{matrix} \end{matrix}

3、继续对两个子区域调用步骤1~2，直到满足停止条件。

$M$ $R_1,R_2,...,R_M$ ，生成决策树：

\begin{matrix} (22) & f (x) = \sum_{m = 1}^{M} {\hat{c}}_{m} I (x \in R_{m}) \end{matrix}

三、构建过程 - 分类树

输入：训练数据集D，停止计算的条件

输出：CART决策树

主要过程：

$A=a$ $D_1$ $D_2$ $A=a$ $Gini(D, A)$ 。

2、对所有可能的特征及其取值，选择基尼指数最小的特征及其取值，作为最优特征及最优切分点。根据最优特征及最优切分点，从现节点生成两个子节点，将训练数据集依特征分配到两个子节点中去。

3、继续对两个子区域调用步骤1~2，直到满足停止条件。

4、生成CART决策树。

小结

算法	场景	树结构	特征选择	连续值	缺失值	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益比	支持	支持	支持
CART	分类，回归	二叉树	基尼指数，MSE	支持	支持	支持

集成学习

集成学习是通过训练若干个弱学习器，通过一定的组合策略，从而形成一个强学习器。按照基学习器之间是否存在依赖关系，可以分为两类：

基学习器之间不存在强依赖关系：基学习器可以并行生成，代表算法是bagging系列算法。
基学习器存在强依赖关系：基学习器需要串行生成，代表算法是boosting系列算法。

Bagging

Bagging(bootstrap aggregating)是并行式集成学习方法的代表。

$X_1,X_2,...X_N$ $f_i(x)$ ，最终分类结果由N个分类器投票得出：

\begin{matrix} (23) & f (x) = s i g n (\frac{1}{N} \sum_{i = 1}^{N} f_{i} (x)) \end{matrix}

算法流程如下：

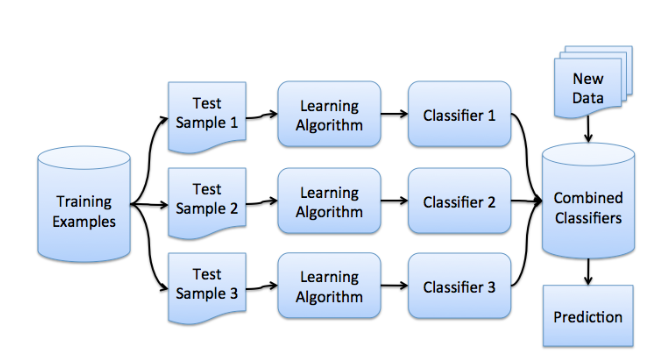
bagging

$Y_1,Y_2,...,Y_N$ $Y=\frac{1}{N}\sum_{i=1}^{N}Y_i$ $\mu$ $\sigma ^2$ 。则bagging的期望预测为：

\begin{matrix} (24) & E (Y) = E (\frac{1}{N} \sum_{i = 1}^{N} Y_{i}) = \frac{1}{N} E (\sum_{i = 1}^{N} Y_{i}) = E (Y_{i}) \approx μ \end{matrix}

说明bagging模型预测的期望近似于单模型的期望，意味着bagging模型的bias与单模型的bias近似，所以bagging通常选择偏差低的强学习器。

$0 < \rho < 1$ ，则bagging模型的方差为：

\begin{matrix} (25) & \begin{aligned} V a r (Y) & = V a r (\frac{1}{N} \sum_{i = 1}^{N} Y_{i}) \\ = \frac{1}{N^{2}} V a r (\sum_{i = 1}^{N} Y_{i}) \\ = \frac{1}{N^{2}} C o v (\sum_{i = 1}^{N} Y_{i}, \sum_{i = 1}^{N} Y_{i}) \\ = \frac{1}{N^{2}} (\sum_{i = 1}^{N} V a r (Y_{i}) + \sum_{i \neq j}^{N} C o v (Y_{i}, Y_{j})) \\ = \frac{1}{N^{2}} (N σ^{2} + N (N - 1) ρ σ^{2}) \\ = ρ σ^{2} + \frac{1 - ρ}{N} σ^{2} \end{aligned} \end{matrix}

$Var(Y)\approx \rho \sigma^2$ ，bagging能降低整体预测结果的variance，而对bias优化有限。

Boosting

Adaboost

需要解决的两个问题：

每一轮如何改变训练数据的权值或概率分布？
提高前一轮被错误分类的样本的权值，降低被正确分类的样本的权值。
如何将弱分类器组合成一个强分类器？
加权多数表决。加大误差率低的分类器的权值，较小误差率高的分类器的权值。

分类

$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$ $x_i \in X \subseteq R ^N,y_i \in Y =\{-1,+1\}$ ；弱学习器算法。

$G(x)$ 。

算法步骤如下：

初始化训练数据的权值分布（该值影响分类误差率）
$D_1=(w_{11},...,w_{1i},...,w_{1N}) \\ w_{1i}=\frac{1}{N} \\ i=1,2,...,N$
$m=1,2,...,M$

$D_m$ 的训练数据集学习，得到基本分类器：

\begin{matrix} (26) & G_{m} (x) : X \to {- 1, + 1} \end{matrix}

计算分类误差率
$G_m(x)$ 在训练数据集上的分类误差率：
$\begin{matrix} (27) & e_{m} = \sum_{i = 1}^{N} P (G_{m} (x_{i}) \neq y_{i}) = \sum_{i = 1}^{N} w_{m i} I (G_{m} (x_{i}) \neq y_{i}) \end{matrix}$
$G_m(x)$ 的系数：
$\begin{matrix} (28) & α_{m} = \frac{1}{2} \log \frac{1 - e_{m}}{e_{m}} \end{matrix}$
更新训练数据集的权值分布

\begin{matrix} (29) & \begin{aligned} D_{m + 1} & = (w_{m + 1, 1}, . . ., w_{m + 1, i}, . . ., w_{m + 1, N}) \\ w_{m + 1, i} & = \frac{w_{m i}}{Z_{m}} e^{- α_{m} y_{i} G_{m} (x_{i})}, i = 1, 2, . . ., N \end{aligned} \end{matrix}

$Z_m$ 是规范化因子：

\begin{matrix} (30) & Z_{m} = \sum_{i = 1}^{N} w_{m i} e^{- α_{m} y_{i} G_{m} (x_{i})} \end{matrix}

$D_{m+1}$ 成为一个概率分布。

构建弱分类器的线性组合
$\begin{matrix} (31) & f (x) = \sum_{m = 1}^{M} α_{m} G_{m} (x) \end{matrix}$
最终分类器
$\begin{matrix} (32) & \begin{aligned} G (x) & = s i g n (f (x)) \\ = s i g n (\sum_{m = 1}^{M} α_{m} G_{m} (x)) \end{aligned} \end{matrix}$

回归

$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$ $x_i \in X \subseteq R ^N,y_i \in Y \subseteq R$ ；弱学习器算法。

$G(x)$ 。

算法步骤如下：

初始化训练数据的权值分布（该值影响分类误差率）
$D_1=(w_{11},...,w_{1i},...,w_{1N}) \\ w_{1i}=\frac{1}{N} \\ i=1,2,...,N$
$m=1,2,...,M$
- $D_m$ $G_m(x)$
- 计算训练集上的最大误差
  $\begin{matrix} (33) & E_{m} = m a x | y_{i} - G_{m} (x_{i}) | \end{matrix}$
- 计算单个样本的相对误差
  $\begin{matrix} (34) & \begin{matrix} 如果是线性误差，则 e_{m i} = \frac{| y_{i} - G_{m} (x_{i}) |}{E_{m}} \\ 如果是平方误差，则 e_{m i} = \frac{(y_{i} - G_{m} (x_{i}))^{2}}{E_{m}^{2}} \\ 如果是指数误差，则 e_{m i} = 1 - e^{\frac{- | y_{i} - G_{m} (x_{i}) |}{E_{m}}} \end{matrix} \end{matrix}$
- $G_m(x)$ 在训练数据集上的误差率：
  $\begin{matrix} (35) & e_{m} = \sum_{i = 1}^{m} w_{m i} e_{m i} \end{matrix}$
- 计算弱分类器的系数
  $\begin{matrix} (36) & α_{m} = \frac{e_{m}}{1 - e_{m}} \end{matrix}$
- 更新训练数据集的权值分布
  $\begin{matrix} (37) & \begin{aligned} D_{m + 1} & = (w_{m + 1, 1}, . . ., w_{m + 1, i}, . . ., w_{m + 1, N}) \\ w_{m + 1, i} & = \frac{w_{m i}}{Z_{m}} α_{m}^{1 - e_{m i}}, i = 1, 2, . . ., N \end{aligned} \end{matrix}$
  $Z_m$ 是规范化因子：
  $\begin{matrix} (38) & Z_{m} = \sum_{i = 1}^{m} w_{m i} α_{m}^{1 - e_{m, i}} \end{matrix}$
  $D_{m+1}$ 成为一个概率分布。
构建弱分类器的线性组合，得到最终的强学习器

\begin{matrix} (39) & f (x) = \sum_{m = 1}^{M} (\ln \frac{1}{α_{m}}) G_{m} (x) \end{matrix}

BDT

BDT（boosting decision tree），提升决策树。

分类

将Adaboost分类算法中的基本分类器限定为二分类树模型即可。

回归

$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}, x_i \in X \subseteq R^n, y_i \in Y \subseteq R$

$f_M(x)$ ，基模型为树模型

算法步骤：

定义模型
$\begin{matrix} (40) & \begin{matrix} f_{M} (x) = \sum_{m = 1}^{M} T_{m} (x; Θ_{m}) \\ T_{m} (x; Θ_{m}) = \sum_{j = 1}^{J_{m}} c_{j} I (x \in R_{j}) \end{matrix} \end{matrix}$
$\Theta_m={(R_1,c_1),(R_2,c_2),...,(R_{J_m},c_{J_m})}$ $J_m$ $m$ 棵回归树的叶子节点数（也可认为是树的复杂度）。
定义损失函数
$m$ 轮的损失为：
$\begin{matrix} (41) & \begin{aligned} L [y, f_{m} (x)] & = L [y, f_{m - 1} (x) + T_{m} (x; Θ_{m})] \\ = [y - f_{m - 1} (x) - T_{m} (x; Θ_{m})]^{2} \\ = [r - T_{m} (x; Θ_{m})]^{2} \\ 其中， r & = y - f_{m - 1} (x) 是当前模型拟合数据的残差 \end{aligned} \end{matrix}$
因此，对回归提升树来讲，只需拟合当前模型的残差即可。
$m=1,2,...,M$
- 计算残差：
  $\begin{matrix} (42) & r_{m i} = y_{i} - f_{m - 1} (x), i = 1, 2, . . ., N \end{matrix}$
- $m$ $T_m(x;\Theta_m)$
  $(x_1,r_{m1}),(x_2,r_{m2}),...,(x_N,r_{mN})$ $T_m(x;\Theta_m)$
- 更新模型
  $\begin{matrix} (43) & f_{m} (x) = f_{m - 1} (x) + T (x; Θ_{m}) \end{matrix}$
生成最终的回归问题提升树
$\begin{matrix} (44) & f_{M} (x) = \sum_{m = 1}^{M} T_{m} (x; Θ_{m}) \end{matrix}$

GBDT

GBDT（gradient boosting decision tree），梯度提升决策树。

回归

以回归为例，解释GBDT原理。

解释一
$x_i$ $y_i$ ：
$\begin{matrix} (45) & \hat{y_{i}} = F_{M} (x_{i}) = \sum_{m = 1}^{M} h_{m} (x_{i}) \end{matrix}$
根据boosting算法：
$\begin{matrix} (46) & F_{m} (x) = F_{m - 1} (x) + h_{m} (x) \end{matrix}$
$F_{m-1}$ $h_m$ $l_m$ 降低，即：
$\begin{matrix} (47) & h_{m} = \arg min_{h} l_{m} = \arg min_{h} \sum_{i = 1}^{n} l (y_{i}, F_{m - 1} (x_{i}) + h (x_{i})) \end{matrix}$
根据泰勒展开公式：
$\begin{matrix} (48) & f (x_{0} + Δ x) \approx f (x_{0}) + Δ x * f^{^{'}} (x_{0}) \end{matrix}$
$l_m$ 一阶展开后可得：
$\begin{matrix} (49) & \begin{aligned} l (y_{i}, F_{m - 1} (x_{i}) + h_{m} (x_{i})) & \approx l (y_{i}, F_{m - 1} (x_{i})) + h_{m} (x_{i}) * {[\frac{\partial l (y_{i}, F (x_{i}))}{\partial F (x_{i})}]}_{F = F_{m - 1}} \\ = l (y_{i}, F_{m - 1} (x_{i})) + h_{m} (x_{i}) * g_{i} \\ 其中， g_{i} & = {[\frac{\partial l (y_{i}, F (x_{i}))}{\partial F (x_{i})}]}_{F = F_{m - 1}} \end{aligned} \end{matrix}$
$l(y_i, F_{m-1}(x_i))$ $l_m$ $h_m$ 为：
$\begin{matrix} (50) & \begin{aligned} h_{m} & \approx \arg min_{h} \sum_{i = 1}^{n} h (x_{i}) g_{i} \\ = \arg min_{h} [h (x_{1}), h (x_{2}), . . ., h (x_{n})] \cdot [\begin{array}{c} g_{1} \\ g_{2} \\ . . . \\ g_{n} \end{array}] \\ = \arg min_{h} \vec{h (x)} \cdot \vec{g} \end{aligned} \end{matrix}$
$\vec{h(x)}=-\vec{g}$ $\vec{h(x)}\cdot \vec{g}$ $l_m$ 取得最小值。因此：
$h_m$ $-\vec{g}$ $r_{mi}$ 为：
$\begin{matrix} (51) & r_{m i} = g_{i} = {[\frac{\partial l (y_{i}, F (x_{i}))}{\partial F (x_{i})}]}_{F = F_{m - 1}} \end{matrix}$
解释二
$l_m$ 下降，根据梯度下降原理：
$\begin{matrix} (52) & f_{m} = f_{m - 1} - \frac{\partial l (y, f_{m - 1})}{\partial f_{m - 1}} \end{matrix}$
而根据加法模型：
$\begin{matrix} (53) & f_{m} = f_{m - 1} + h_{m} \end{matrix}$
$l_m$ $h_m$ $-\frac{\partial l(y,f_{m-1})}{\partial f_{m-1}}$ 即可：
$\begin{matrix} (54) & h_{m} \to - \frac{\partial l (y, f_{m - 1})}{\partial f_{m - 1}} \end{matrix}$

二分类

$(0,1)$ ，预测结果为：

\begin{matrix} (55) & \begin{matrix} c l a s s = {\begin{cases} 0 & if \hat{y} < θ \\ 1 & if \hat{y} >= θ \end{cases} \\ 其 中 ， θ 为 二 分 类 判 断 阈 值 \end{matrix} \end{matrix}

定义模型
$x_i$ ，模型输出为：

\begin{matrix} (56) & \begin{matrix} \hat{y_{i}} = \frac{1}{1 + e^{- F_{M} (x_{i})}} \\ 其 中 ， F_{M} (x_{i}) = \sum_{m = 1}^{M} h_{m} (x_{i}) ， h_{m} (x) 为 每 次 迭 代 的 树 模 型 \end{matrix} \end{matrix}

模型初始化为：

\begin{matrix} (57) & F_{0} (x) = h_{0} (x) = l o g \frac{\sum_{i = 1}^{N} y_{i}}{\sum_{i = 1}^{N} (1 - y_{i})} \end{matrix}

定义损失函数
损失函数使用交叉熵损失，即：
$\begin{matrix} (58) & L (y_{i}, \hat{y_{i}}) = - y_{i} l o g \hat{y_{i}} - (1 - y_{i}) l o g (1 - \hat{y_{i}}) \end{matrix}$
求负梯度
因为GBDT拟合的是损失函数关于模型的负梯度，求导可得：

\begin{matrix} (59) & \begin{aligned} - \frac{\partial L (y_{i}, \hat{y_{i}})}{\partial F (x_{i})} & = - \frac{\partial {- y_{i} l o g \hat{y_{i}} - (1 - y_{i}) l o g (1 - \hat{y_{i}})}}{\partial F (x_{i})} \\ = - {- y_{i} \frac{1}{\hat{y_{i}}} \frac{\partial \hat{y_{i}}}{\partial F (x_{i})} - (1 - y_{i}) \frac{- 1}{1 - \hat{y_{i}}} \frac{\partial \hat{y_{i}}}{\partial F (x_{i})}} \\ = - {- \frac{y_{i}}{\hat{y_{i}}} \hat{y_{i}} (1 - \hat{y_{i}}) - \frac{y_{i} - 1}{1 - \hat{y_{i}}} \hat{y_{i}} (1 - \hat{y_{i}})} \\ = {(\frac{y_{i}}{\hat{y_{i}}} + \frac{y_{i} - 1}{1 - \hat{y_{i}}}) \hat{y_{i}} (1 - \hat{y_{i}})} \\ = y_{i} - \hat{y_{i}} \end{aligned} \end{matrix}

$L(y_i,F(x_i))$ $F{(x_i)}$ 的的负梯度值（伪残差）为：

\begin{matrix} (60) & r_{m i} = - {[\frac{\partial {- y_{i} l o g \hat{y_{i}} - (1 - y_{i}) l o g (1 - \hat{y_{i}})}}{\partial F (x_{i})}]}_{F (x) = F_{m - 1} (x)} = y_{i} - \frac{1}{1 + e^{- F_{m - 1} (x_{i})}} \end{matrix}

$m=1,2,...,M$
- $i=1,2,...,N$
  $r_{mi}=y_i-\frac{1}{1+e^{-F_{m-1}(x_i)}}$
- $h_m(x)$
  $(x_i,r_{mi})$ $R_{mj}，j=1,2,...,J_m$ $J_m$ 为第m棵回归树叶子节点的个数。
- $J_m$ $j=1,2,...,J_m$ ，计算出最佳拟合值
  $\begin{matrix} (61) & \begin{aligned} c_{m j} & = \underset{c}{a r g m i n} \sum_{x_{i} \in R_{m j}} L (y_{i}, F_{m - 1} (x_{i}) + c) \\ \approx \frac{\sum_{x_{i} \in R_{m, j}} r_{m, i}}{\sum_{x_{i} \in R_{m, j}} (y_{i} - r_{m, i}) (1 - y_{i} + r_{m, i})} \end{aligned} \end{matrix}$
  由于上式没有闭式解，所以采用近似值代替，代替过程如下：
  $\begin{matrix} (62) & \begin{aligned} G (c) & = \sum_{x_{i} \in R_{m j}} L (y_{i}, F_{m - 1} (x_{i}) + c) \\ \approx \sum_{x_{i} \in R_{m j}} L (y_{i}, F_{m - 1} (x_{i})) + \sum_{x_{i} \in R_{m j}} c \cdot \frac{\partial L (y_{i}, F_{m - 1} (x_{i}))}{\partial F_{m - 1} (x_{i})} + \sum_{x_{i} \in R_{m j}} \frac{1}{2} \cdot c^{2} \cdot \frac{\partial^{2} L (y_{i}, F_{m - 1} (x_{i}))}{\partial F_{m - 1}^{2} (x_{i})} \\ \frac{d G}{d c} & = \sum_{x_{i} \in R_{m j}} \frac{\partial L (y_{i}, F_{m - 1} (x_{i}))}{\partial F_{m - 1} (x_{i})} + \sum_{x_{i} \in R_{m j}} c \cdot \frac{\partial^{2} L (y_{i}, F_{m - 1} (x_{i}))}{\partial F_{m - 1}^{2} (x_{i})} \\ 令 \frac{d G}{d c} & = 0 ，此时的 c 使得 G (c) 最小，得： \\ c & = \frac{\sum_{x_{i} \in R_{m j}} \frac{\partial L (y_{i}, F_{m - 1} (x_{i}))}{\partial F_{m - 1} (x_{i})}}{\sum_{x_{i} \in R_{m j}} \frac{\partial^{2} L (y_{i}, F_{m - 1} (x_{i}))}{\partial F_{m - 1}^{2} (x_{i})}} \\ = \frac{\sum_{x_{i} \in R_{m j}} r_{m, i}}{\sum_{x_{i} \in R_{m j}} \hat{y_{i}} (1 - \hat{y_{i}})} \\ = & \frac{\sum_{x_{i} \in R_{m, j}} r_{m, i}}{\sum_{x_{i} \in R_{m, j}} (y_{i} - r_{m, i}) (1 - y_{i} + r_{m, i})} \end{aligned} \end{matrix}$
- $F_m(x)$
  $\begin{matrix} (63) & F_{m} (x) = F_{m - 1} (x) + \sum_{j = 1}^{J_{m}} c_{m, j} I (x \in R_{m, j}) \end{matrix}$
$F_M(x)$
$\begin{matrix} (64) & F_{M} (x) = F_{0} (x) + \sum_{m = 1}^{M} \sum_{j = 1}^{J_{m}} c_{m, j} I (x \in R_{m, j}) \end{matrix}$
结果预测
$\begin{matrix} (65) & \begin{matrix} P (Y = 1 | x) = \frac{1}{1 + e^{- F_{M} (x)}} \\ P (Y = 0 | x) = 1 - P (Y = 1 | x) \end{matrix} \end{matrix}$

多分类

$(x,\underbrace{0,.,1,.,0}_k)$ ，label中只有一个维度为1。

模型最终生成K棵集成决策树。

定义模型
给定输入x，属于第k类的概率为：
$\begin{matrix} (66) & \begin{matrix} P (y = k | x) = P_{k} = \frac{e^{F_{k} (x)}}{\sum_{i = 1}^{K} e^{F_{i} (x)}} \\ 预测类别 = \underset{k}{a r g m a x} P (y = k | x) = \underset{k}{a r g m a x} \frac{e^{F_{k} (x)}}{\sum_{i = 1}^{K} e^{F_{i} (x)}} \\ 其中， F_{k} (x) 为第 k 棵集成树 \end{matrix} \end{matrix}$
$q=1,2,...,K$ ，模型初始化为：
$\begin{matrix} (67) & F_{0 q} (x) = l o g \frac{\sum_{i = 1}^{N} y_{i q}}{\sum_{i = 1}^{N} (1 - y_{i q})} \end{matrix}$
定义损失函数
$\begin{matrix} (68) & L (y_{i}, {\hat{P}}_{i}) = - \sum_{q = 1}^{K} y_{q} l o g P (y = q | x_{i}) = - \sum_{q = 1}^{K} y_{q} l o g \frac{e^{F_{q} (x_{i})}}{\sum_{j = 1}^{K} e^{F_{j} (x_{i})}} \end{matrix}$
$F_q(x)$ 的负梯度
$\begin{matrix} (69) & \begin{aligned} - \frac{\partial L (y_{q}, {\hat{P}}_{q})}{\partial F_{q} (x)} & = \frac{\partial [\sum_{i = 1}^{K} y_{i} F_{i} (x) - \sum_{i = 1}^{K} y_{i} \cdot l o g \sum_{j = 1}^{K} e^{F_{j} (x)}]}{\partial F_{q} (x)} \\ = y_{q} - \sum_{i = 1}^{K} y_{i} \cdot \frac{e^{F_{q} (x)}}{\sum_{j = 1}^{K} e^{F_{j} (x)}} \\ = y_{q} - {\hat{P}}_{q} \cdot \sum_{i = 1}^{K} y_{i} \\ = y_{q} - {\hat{P}}_{q} \end{aligned} \end{matrix}$
因此，第m轮第i个样本对应的第q个类别的损失函数负梯度为：
$\begin{matrix} (70) & \begin{aligned} r_{m i q} & = - {[\frac{\partial L (y_{i q}, F_{q} (x_{i}))}{\partial F_{q} (x_{i})}]}_{F_{q} (x) = F_{(m - 1) q} (x)} \\ = {[y_{i q} - \frac{e^{F_{q} (x_{i})}}{\sum_{j = 1}^{K} e^{F_{q} (x_{i})}}]}_{F_{q} (x) = F_{(m - 1) q} (x)} \end{aligned} \end{matrix}$
$m=1,2,..,M$
- $i=1,2,..,N$ $q=1,2,..,K$
- $\large r_{miq}$
- $\large (x,r_{miq})$ $\large R_{mqj},j=1,2,...,J_{mq}$ $J_{mq}$ 为第m棵第q类回归树叶子节点的个数。
- $J_{mq}$ $j=1,2,...,J_{mq}$ ，计算出最佳拟合值
  $\begin{matrix} \begin{matrix} (71) & \begin{aligned} c_{m q j} & = \underset{c}{a r g m i n} \sum_{x_{i} \in R_{m q j}} L (y_{i q}, F_{(m - 1) q} (x_{i}) + c) \\ \approx \frac{\sum_{x_{i} \in R_{m q j}} r_{m i q}}{\sum_{x_{i} \in R_{m q j}} | r_{m i q} | (1 - | r_{m i q} |)} \cdot \frac{K - 1}{K} \end{aligned} \end{matrix} \end{matrix}$
- $F_{mq}(x)$
  $\begin{matrix} (72) & F_{m q} (x) = F_{(m - 1) q} (x) + \sum_{j = 1}^{J_{m q}} c_{m q j} I (x \in R_{m q j}) \end{matrix}$
$F_{Mq},q=1,2...,K$
$\begin{matrix} (73) & F_{M q} (x) = F_{0 q} (x) + \sum_{m = 1}^{M} \sum_{j = 1}^{J_{m q}} c_{m q j} I (x \in R_{m q j}) \end{matrix}$
结果预测
$\begin{matrix} (74) & \begin{matrix} P (y = k | x) = \frac{e^{F_{M k} (x)}}{\sum_{i = 1}^{K} e^{F_{M i} (x)}} \\ 预测类别 = \underset{k}{a r g m a x} \frac{e^{F_{M k} (x)}}{\sum_{i = 1}^{K} e^{F_{M i} (x)}} \end{matrix} \end{matrix}$

总结

集成方法	优点	缺点	示例
bagging	能处理过拟合；能够降低variance；学习器独立，可并行训练；	噪声大时会过拟合；可能会有很多相似的决策树；小数据或低维数据效果一般；	随机森林
boosting	能够降低bias和variance；	容易过拟合；串行训练；	GBDT

Bagging实现

随机森林

假设数据样本数为N，每个样本的属性个数为M，在每个决策树构造过程中，每个节点随机选择m个属性计算最佳分裂方式进行分裂。具体步骤如下：

有放回地随机选择N个样本，用这N个样本来训练一棵决策树。
每个样本有M个属性，在决策树中需要分裂节点时，从这M个属性中随机选取m个属性，一般来说m << M，然后从这m个属性中采用某种策略选择最佳属性作为当前节点的分裂属性。
每棵决策树的每个节点的分裂都按照步骤（2）进行，直到不能分裂为止。
重复建立K棵决策树，然后对预测结果进行一定组合，即可得随机森林模型。

Boosting-GBDT实现

XGBoost

模型概述

\begin{matrix} (75) & \begin{aligned} X G B o o s t & = e X t r e m e + G B D T \\ = e X t r e m e + (G r a d i e n t + B D T) \\ = e X t r e m e + G r a d i e n t + (B o o s t i n g + D e c i s i o n T r e e) \end{aligned} \end{matrix}

$Boosting \to BDT \to GBDT \to X\!G\!Boost$

原理推导

$D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),...,(\mathbf{x}_N,y_N)\}$ $\mathbf{x}_i \in R^M, y_i \in R, |D|=N$

$K$ 个基本树模型组成

定义模型

\begin{matrix} (76) & \begin{matrix} {\hat{y}}_{i} = ϕ (x_{i}) = \sum_{k = 1}^{K} f_{k} (x_{i}) \\ 其 中 ， K 为 决 策 树 个 数 ， f_{k} (x) 为 第 k 棵 决 策 树 \end{matrix} \end{matrix}

决策树定义为：

\begin{matrix} (77) & f (x) = w_{q (x)} \end{matrix}

$q(\mathbf{x})$ $\mathbf{x}$ 叶子节点编号 $R^m \rightarrow \{1,...,T\}，T$ 为决策树叶子节点数目。

$\mathbf{w} \in R^T$ $(w_1, w_2,...,w_T)$ 。

决策树结构图如下所示：

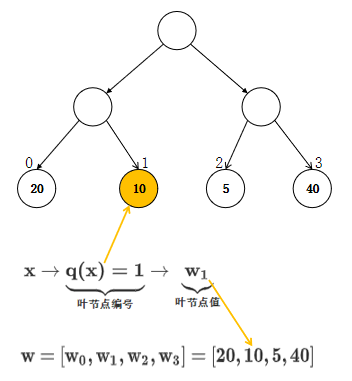
定义损失函数

\begin{matrix} (78) & \begin{matrix} L (ϕ) = \sum_{i} l ({\hat{y}}_{i}, y_{i}) + \sum_{k} Ω (f_{k}) \\ 其 中 ， l ({\hat{y}}_{i}, y_{i}) 为 经 验 风 险 \\ Ω (f) 为 结 构 风 险 ， Ω (f) = γ T + \frac{1}{2} λ ∥ w ∥^{2} = γ T + \frac{1}{2} λ \sum_{j = 1}^{T} w_{j}^{2} \end{matrix} \end{matrix}

$t$ 轮损失函数：

\begin{matrix} (79) & L^{(t)} = \sum_{i = 1}^{N} l (y_{i}, {\hat{y}}_{i}^{(t - 1)} + f_{t} (x_{i})) + Ω (f_{t}) \end{matrix}

$t$ $\mathcal{L}^{\left(t\right)}$ $\hat{y}^{\left(t-1\right)}$ 处的二阶泰勒展开为：

\begin{matrix} (80) & \begin{aligned} L^{(t)} & ≃ \sum_{i = 1}^{n} [l (y_{i}, {\hat{y}}^{(t - 1)}) + \partial_{{\hat{y}}^{(t - 1)}} l (y_{i}, {\hat{y}}^{(t - 1)}) f_{t} (x_{i}) + \frac{1}{2} \partial_{{\hat{y}}^{(t - 1)}}^{2} l (y_{i}, {\hat{y}}^{(t - 1)}) f_{t}^{2} (x_{i})] + Ω (f_{t}) \\ = \sum_{i = 1}^{n} [l (y_{i}, {\hat{y}}^{(t - 1)}) + g_{i} f_{t} (x_{i}) + \frac{1}{2} h_{i} f_{t}^{2} (x_{i})] + Ω (f_{t}) \end{aligned} \end{matrix}

$其中，g_i=\partial_{\hat{y}^{\left(t-1\right)}}l\left(y_i,\hat{y}^{\left(t-1\right)}\right),h_i=\partial^2_{\hat{y}^{\left(t-1\right)}}l\left(y_i,\hat{y}^{\left(t-1\right)}\right)$

$t$ $\mathcal{L}^{\left(t\right)}$ 的二阶泰勒展开移除常数项：

\begin{matrix} (81) & \begin{aligned} {\tilde{L}}^{(t)} & = \sum_{i = 1}^{N} [g_{i} f_{t} (x_{i}) + \frac{1}{2} h_{i} f_{t}^{2} (x_{i})] + Ω (f_{t}) \\ = \sum_{i = 1}^{N} [g_{i} f_{t} (x_{i}) + \frac{1}{2} h_{i} f_{t}^{2} (x_{i})] + γ T + \frac{1}{2} λ \sum_{j = 1}^{T} w_{j}^{2} \end{aligned} \end{matrix}

$其中，T为叶子节点数$

$j$ 样本的下标集合 $I_j=\{i|q\left(\mathbf{x}_i\right)=j\}$ ，则目标函数可表示为 按叶结点 累加的形式：

\begin{matrix} (82) & \begin{aligned} {\tilde{L}}^{(t)} & = \sum_{i = 1}^{n} [g_{i} f_{t} (x_{i}) + \frac{1}{2} h_{i} f_{t}^{2} (x_{i})] + γ T + \frac{1}{2} λ \sum_{j = 1}^{T} w_{j}^{2} \\ = \sum_{j = 1}^{T} [(\sum_{i \in I_{j}} g_{i}) w_{j} + \frac{1}{2} (\sum_{i \in I_{j}} h_{i}) w_{j}^{2}] + \frac{1}{2} λ \sum_{j = 1}^{T} w_{j}^{2} + γ T \\ = \sum_{j = 1}^{T} [(\sum_{i \in I_{j}} g_{i}) w_{j} + \frac{1}{2} (\sum_{i \in I_{j}} h_{i} + λ) w_{j}^{2}] + γ T \end{aligned} \end{matrix}

由于：

\begin{matrix} (83) & w_{j}^{*} = \underset{w_{j}}{\arg min} {\tilde{L}}^{(t)} \end{matrix}

可令：

\begin{matrix} (84) & \frac{\partial {\tilde{L}}^{(t)}}{\partial w_{j}} = 0 \end{matrix}

$j$ 的最优输出值为：

\begin{matrix} (85) & w_{j}^{*} = - \frac{\sum_{i \in I_{j}} g_{i}}{\sum_{i \in I_{j}} h_{i} + λ} \end{matrix}

$j$ $t$ 个决策树损失函数的最小值：

\begin{matrix} (86) & \begin{matrix} {\tilde{L}}^{(t)} (q) = - \frac{1}{2} \sum_{j = 1}^{T} \frac{{(\sum_{i \in I_{j}} g_{i})}^{2}}{\sum_{i \in I_{j}} h_{i} + λ} + γ T \\ 其 中 ， T 为 第 t 轮 决 策 树 的 叶 节 点 数 \end{matrix} \end{matrix}

节点分裂准则

$I_L$ $I_R$ $I=I_L\cup I_R$ ，则分裂后损失减少量由下式得出：

\begin{matrix} (87) & \begin{aligned} L_{s p l i t} & = {\tilde{L}}_{I}^{(t)} - ({\tilde{L}}_{I_{L}}^{(t)} + {\tilde{L}}_{I_{R}}^{(t)}) \\ = - \frac{1}{2} \frac{{(\sum_{i \in I} g_{i})}^{2}}{\sum_{i \in I} h_{i} + λ} + γ - [- \frac{1}{2} \frac{{(\sum_{i \in I_{L}} g_{i})}^{2}}{\sum_{i \in I_{L}} h_{i} + λ} + γ] - [- \frac{1}{2} \frac{{(\sum_{i \in I_{R}} g_{i})}^{2}}{\sum_{i \in I_{R}} h_{i} + λ} + γ] \\ = \frac{1}{2} [\frac{{(\sum_{i \in I_{L}} g_{i})}^{2}}{\sum_{i \in I_{L}} h_{i} + λ} + \frac{{(\sum_{i \in I_{R}} g_{i})}^{2}}{\sum_{i \in I_{R}} h_{i} + λ} - \frac{{(\sum_{i \in I} g_{i})}^{2}}{\sum_{i \in I} h_{i} + λ}] - γ \end{aligned} \end{matrix}

$\mathcal{L}_{split}$ 评估待分裂结点。

XGBoost 节点分裂贪婪查找算法

$\mathcal{L}_{split}$ 查找最优分裂点

$I$ $d$

输出：根据最大score分裂

算法步骤：

$gain\leftarrow 0$

$G\leftarrow\sum_{i\in I}g_i$ $H\leftarrow\sum_{i\in I}h_i$

$k=1$ $d$ do

$G_L \leftarrow 0$ $H_L \leftarrow 0$

$j$ $I$ $\mathbf{x}_{jk}$ ) do

$G_L \leftarrow G_L+g_j$ $H_L \leftarrow H_L+h_j$

$G_R \leftarrow G-G_L$ $H_R=H-H_L$

$score \leftarrow \max\left(score,\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{G^2}{H+\lambda}\right)$

$end$

LightGBM

分裂准则：

数据集 $O$ 特征 $j$ 分裂点 $d$ 分裂后的方差收益为：

\begin{matrix} (88) & \begin{matrix} V_{j | O} (d) = \frac{1}{n_{O}} (\frac{(\sum_{x_{i} \in O; x_{i j} \leq d} g_{i})^{2}}{n_{l | O}^{j} (d)} + \frac{(\sum_{x_{i} \in O; x_{i j} > d} g_{i})^{2}}{n_{r | O}^{j} (d)}) \\ 其 中 ， n_{O} = \sum I [x_{i} \in O], n_{l | O}^{j} (d) = \sum I [x_{i} \in O : x_{i j} \leq d], n_{r | O}^{j} (d) = \sum I [x_{i} \in O : x_{i j} > d] \end{matrix} \end{matrix}

特征 $j$ 的最佳分裂点：

\begin{matrix} (89) & d_{j}^{*} = \underset{d}{a r g m a x} V_{j} (d) \end{matrix}

解释一：基于CART树寻找最优分裂点

$g_i$ 为当前步骤要拟合的值，损失函数使用MSE，分裂后使得损失最小，即：

\begin{matrix} (90) & \begin{aligned} m i n {\sum_{p \in L} (g_{p} - {\bar{g}}_{L})^{2} + \sum_{q \in R} (g_{q} - {\bar{g}}_{R})^{2}} \\ = m i n {\sum_{p \in L} g_{p}^{2} + \sum_{p \in L} {\bar{g}}_{L}^{2} - 2 \sum_{p \in L} g_{p} {\bar{g}}_{L} + \sum_{q \in R} g_{q}^{2} + \sum_{q \in R} {\bar{g}}_{R}^{2} - 2 \sum_{q \in R} g_{q} {\bar{g}}_{R}} \\ = m i n {- \sum_{p \in L} {\bar{g}}_{L}^{2} - \sum_{q \in R} {\bar{g}}_{R}^{2}} \\ = m a x {\sum_{p \in L} {\bar{g}}_{L}^{2} + \sum_{q \in R} {\bar{g}}_{R}^{2}} \\ = m a x {n (\frac{1}{n} \sum_{p \in L} g_{p})^{2} + m (\frac{1}{m} \sum_{q \in R} g_{q})^{2}} \\ = m a x {\frac{(\sum_{p \in L} g_{p})^{2}}{n} + \frac{(\sum_{q \in L} g_{q})^{2}}{m}} \\ L 和 R 分 别 为 分 裂 后 的 左 右 子 集 \\ {\bar{g}}_{L} 和 {\bar{g}}_{R} 分 别 为 左 右 子 集 g 的 均 值 \end{aligned} \end{matrix}

解释二：参考XGBoost的信息增益

\begin{matrix} (91) & \begin{aligned} m a x [\frac{{(\sum_{i \in I_{L}} g_{i})}^{2}}{\sum_{i \in I_{L}} h_{i} + λ} + \frac{{(\sum_{i \in I_{R}} g_{i})}^{2}}{\sum_{i \in I_{R}} h_{i} + λ} - \frac{{(\sum_{i \in I} g_{i})}^{2}}{\sum_{i \in I} h_{i} + λ}] \\ = m a x [\frac{{(\sum_{i \in I_{L}} g_{i})}^{2}}{\sum_{i \in I_{L}} h_{i} + λ} + \frac{{(\sum_{i \in I_{R}} g_{i})}^{2}}{\sum_{i \in I_{R}} h_{i} + λ}] \\ = m a x [\frac{{(\sum_{i \in I_{L}} g_{i})}^{2}}{\sum_{i \in I_{L}} h_{i}} + \frac{{(\sum_{i \in I_{R}} g_{i})}^{2}}{\sum_{i \in I_{R}} h_{i}}] \end{aligned} \end{matrix}

$h_i$ $V_{j|O}(d)$ 等价。

GOSS(Gradient based One Side Sampling) - 样本下采样
- $a\%$ 个较大梯度值的样本
- $1-a\%$ $b\%$ 个样本
- 对小梯度样本，在计算信息增益时扩大一定倍数

由于梯度较大的数据实例在信息增益的计算中起着更重要的作用，所以GOSS可以在较小的数据量下获得相当准确的信息增益估计。

EFB(Exclusive Feature Bundling) - 独立特征合并
解决数据稀疏的问题。在稀疏特征空间中，许多特征都是互斥的，也就是它们几乎不同时取非0值。因此，可以安全地把这些互斥特征绑到一起形成一个特征。

算法架构

预备知识

信息量

熵（Entropy）

条件熵

信息增益

信息增益比

基尼指数

自助法

Bias-Variance Trade-off

决策树

概述

ID3

C4.5

CART

小结

集成学习

Bagging

Boosting

Adaboost

分类

回归

BDT

分类

回归

GBDT

回归

二分类

多分类

总结

Bagging实现

随机森林

Boosting-GBDT实现

XGBoost

模型概述

原理推导

LightGBM

参考资料