相似度的度量方法
度量的基本要求
相似性的度量方法必须满足拓扑学中的度量空间的基本条件。假设
非负性
对称性
三角不等式
皮尔逊相关系数
余弦相似度
协同过滤
简介
协同过滤(Collaborative Filtering,CF)推荐算法是通过在用户的行为中寻找特定的模式,并通过该模式为用户产生有效推荐的算法。该算法依赖系统中用户的行为数据,通过对用户历史行为数据的挖掘发现用户的偏好,基于不同的偏好对用户进行群组划分并推荐品味相似的物品。
下图为模拟数据,后续将根据该数据进行模拟计算:

基于物品的协同过滤
根据物品相似度进行计算。例如,当用户购买了一个物品后,向其推荐该物品的相似物品。
如下图示例:

因为物品A和物品C都被两个用户(用户A和用户B)购买过,因此这两个物品比较相似。对用户C,因为购买过物品A,此时可以向其推荐物品C。
基于用户的协同过滤
根据用户行为(如购买记录、电影评分等),找到行为相似的客户,然后对于当前用户,利用其相似用户的购买行为进行推荐。
如下图示例:
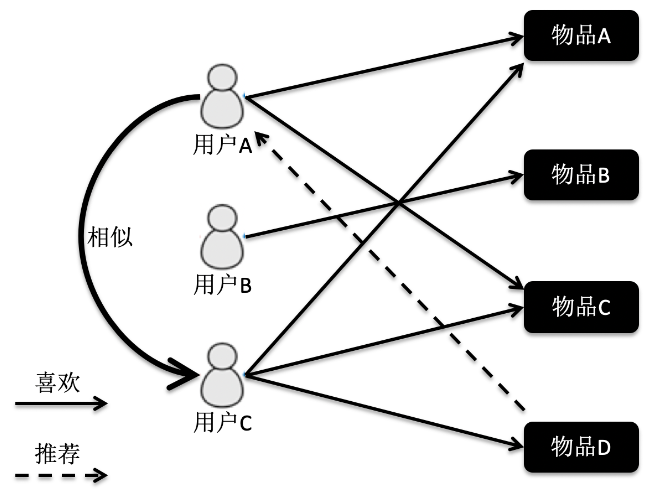
用户A购买了{物品A、物品C},用户C购买了{物品A、物品C、物品D},两个用户比较类似。用户A没有购买物品D,因此可以向其推荐。
计算过程
相关符号定义如下:
以下计算基于余弦相似度进行计算。
基于物品的协同过滤
物品相似度矩阵
用户物品推荐矩阵
对给定的用户
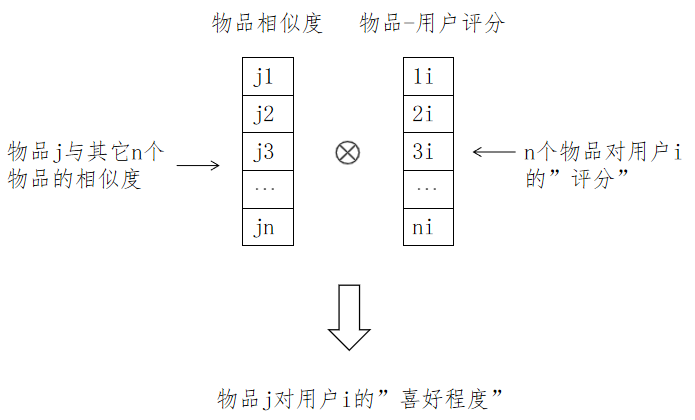
公式如下:
基于用户的协同过滤
通俗解释:如果想判断阿Q对樱桃键盘的喜爱程度,首先计算未庄所有人对樱桃键盘的喜爱程度,其次计算未庄人与阿Q的相似度,最后,将相似度作为权重,与喜爱程度相乘,得到阿Q对樱桃键盘的喜爱程度。
用户相似度矩阵
用户物品推荐矩阵
对给定的用户
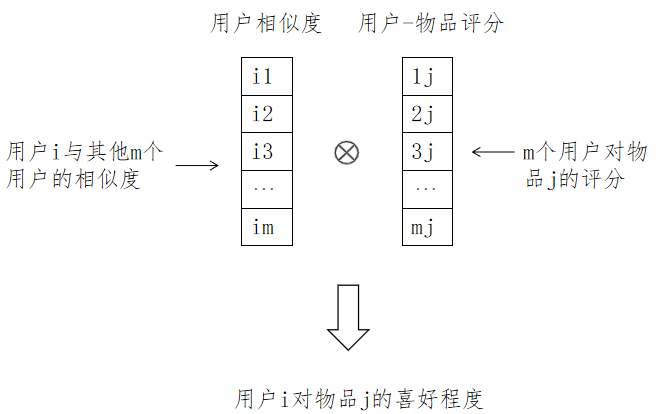
公式如下:
示例代码