感知机模型简介

感知机（perceptron）是二分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取值为$\{+1,-1\}$$\{+1,-1 \}$。感知机对应于输入空间（特征空间）中将实例划分为正负两类的分离超平面，属于判别模型。

定义 (感知机） 假设输入空间（特征空间 ) 是 $\mathcal{X}\subseteq {\mathbf{R}}^n$$\mathcal{X} \subseteq \mathbf{R}^{n}$, 输出空间是 $\mathcal{Y}=\{+1,-1\}$$\mathcal{Y}=\{+1,-1\}$ 。 输入 $x\in \mathcal{X}$$x \in \mathcal{X}$ 表示实例的特征向量, 对应于输入空间 (特征空间 ) 的点; 输出 $y\in \mathcal{Y}$$y \in \mathcal{Y}$ 表示实例的类别。由输入空间到输出空间的如下函数称为感知机：

其中, $w$$w$ 和 $b$$b$ 为感知机模型参数, $w\in {\mathbf{R}}^n$$w \in \mathbf{R}^{n}$ 叫作权值 ( weight ) 或权值向 量( weight vector ), $b\in \mathbf{R}$$b \in \mathbf{R}$ 叫作偏置 ( bias ) , $w\cdot x$$w \cdot x$ 表示 $w$$w$ 和 $x$$x$ 的内积。 $\mathrm{sign}$$\operatorname{sign}$ 是符号函数, 即

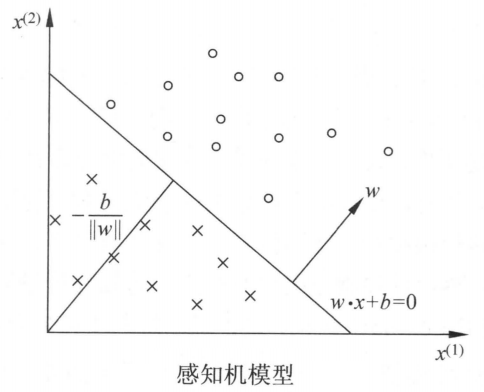
感知机学习策略

空间${\mathbf{R}}^n$$\mathbf{R}^{n}$中任意一点$x_0$$x_0$到超平面$S$$S$的距离：

对误分类的数据$(x_i,y_i)$$(x_i, y_i)$来说：

因此，误分类点$x_i$$x_i$到超平面$S$$S$的距离是：

假设超平面$S$$S$的误分类点集合为$M$$M$，那么所有误分类点到超平面$S$$S$的总距离为：

根据以上推导，可得出感知机的损失函数：

给定训练数据集 $T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$$T=\{(x_1,y_1), (x_2,y_2), \cdots , (x_N, y_N) \}$，其中，$x_i\in \mathcal{X}={\mathbf{R}}^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots ,N$$x_{i} \in \mathcal{X}=\mathbf{R}^{n}, y_{i} \in \mathcal{Y}=\{+1,-1\}, i=1,2, \cdots, N$。感知机$\mathrm{sign}(w\cdot x+b)$$\operatorname{sign}(w \cdot x+b)$学习的损失函数定义为：

感知机学习算法

原始形式

优化目标：

采用梯度下降法进行优化，损失函数的梯度为：

随机选取一个误分类点$(x_i,y_i)$$(x_i, y_i)$，对$w,b$$w,b$进行更新：

$\text{算}\text{法}1.1（\text{感}\text{知}\text{机}\text{学}\text{习}\text{的}\text{原}\text{始}\text{形}\text{式}）$$算法 1.1 （感知机学习的原始形式）$

$\begin{array}{c}\text{输}\text{入}：\text{训}\text{练}\text{数}\text{据}\text{集}T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}，\text{其}\text{中}，x_i\in \mathcal{X}\subseteq {\mathbf{R}}^n，y_i\in \mathcal{Y}=\{-1,+1\}，i=1,2,\cdots ,N；\\ \text{学}\text{习}\text{率}\eta (0<\eta \le 1)\end{array}$$输入：训练数据集T=\{(x_1,y_1),(x_2,y_2),\cdots, (x_N,y_N) \}， 其中，x_i \in \mathcal{X} \subseteq \mathbf{R}^{n}，y_i \in \mathcal{Y}=\{-1,+1 \}，i=1,2,\cdots,N；\\ \quad \quad \; 学习率\eta(0<\eta \leq 1)$

$\text{输}\text{出}：w,b；\text{感}\text{知}\text{机}\text{模}\text{型}f(x)=\mathrm{sign}(w\cdot x+b)$$输出：w, b；感知机模型 f(x)=\operatorname{sign}(w \cdot x+b)$

$(1)\text{选}\text{取}\text{初}\text{值}{w}_0，b_0$$(1) \; 选取初值 w_0， b_0$

$(2)\text{在}\text{训}\text{练}\text{集}\text{中}\text{选}\text{取}\text{数}\text{据}（x_i,y_i）$$(2) \; 在训练集中选取数据（x_i,y_i）$

$(3)\text{如}\text{果}{y}_i(w\cdot x_i+b)\le 0:$$(3) \; 如果 \; y_i(w \cdot x_i + b) \leq 0 \; :$

$\begin{array}{c}w\leftarrow w+\eta y_i{x}_i\\ b\leftarrow b+\eta y_i\end{array}$$w \leftarrow w+\eta y_{i} x_{i} \\ b \leftarrow b+\eta y_{i}$

$(4)\text{转}\text{至}(2)，\text{直}\text{至}\text{训}\text{练}\text{集}\text{中}\text{没}\text{有}\text{误}\text{分}\text{类}\text{点}$$(4) \; 转至(2)，直至训练集中没有误分类点$

对偶形式

基本想法是：将$w$$w$和$b$$b$表示为实例$x_i$$x_i$和标记$y_i$$y_i$的线性组合的形式，通过求解其系数而求得$w$$w$和$b$$b$。不失一般性，在$\text{算}\text{法}1.1$$算法 1.1$中可假设初始值$w_0,b_0$$w_0,b_0$均为0。对分类点$(x_i,y_i)$$(x_i,y_i)$通过

$\begin{array}{c}w\leftarrow w+\eta y_i{x}_i\\ b\leftarrow b+\eta y_i\end{array}$$w \leftarrow w+\eta y_{i} x_{i} \\ b \leftarrow b+\eta y_{i}$

逐步修改$w,b$$w,b$。

设修改$n$$n$次，则$w,b$$w,b$关于$(x_i,y_i)$$(x_i,y_i)$的增量分别是${\alpha }_i{y}_i{x}_i$$\alpha_i y_i x_i$和${\alpha }_i{y}_i$$\alpha_i y_i$，这里${\alpha }_i=n_i\eta$$\alpha_i = n_i \eta$。从学习过程中不难看出，最后学习到的$w,b$$w,b$可以分别表示为：

其中，${\alpha }_i\ge 0，i=1,2,\cdots ,N$$\alpha_i \geq 0，i=1,2,\cdots,N$，当$\eta =1$$\eta = 1$时，${\alpha }_i$$\alpha_i$表示第$i$$i$个实例点由于误分类而进行更新的次数。

$\text{由}{\alpha }_i\text{定}\text{义}\text{可}\text{知}，{\alpha }_{i+1}=\eta (n_i+1)=\eta n_i+\eta ={\alpha }_i+\eta$$由 \alpha_i定义可知，\alpha_{i+1} = \eta (n_i +1) = \eta n_i + \eta = \alpha_i + \eta$

$\text{算}\text{法}1.2（\text{感}\text{知}\text{机}\text{学}\text{习}\text{的}\text{对}\text{偶}\text{形}\text{式}）$$算法 1.2 （感知机学习的对偶形式）$

$\begin{array}{c}\text{输}\text{入}：\text{训}\text{练}\text{数}\text{据}\text{集}T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}，\text{其}\text{中}，x_i\in \mathcal{X}\subseteq {\mathbf{R}}^n，y_i\in \mathcal{Y}=\{-1,+1\}，i=1,2,\cdots ,N；\\ \text{学}\text{习}\text{率}\eta (0<\eta \le 1)\end{array}$$输入：训练数据集T=\{(x_1,y_1),(x_2,y_2),\cdots, (x_N,y_N) \}， 其中，x_i \in \mathcal{X} \subseteq \mathbf{R}^{n}，y_i \in \mathcal{Y}=\{-1,+1 \}，i=1,2,\cdots,N；\\ \quad \quad \; 学习率\eta(0<\eta \leq 1)$

$\text{输}\text{出}：w,b；\text{感}\text{知}\text{机}\text{模}\text{型}f(x)=\mathrm{sign}(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b)，\text{其}\text{中}，\alpha =({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N{)}^T$$输出：w, b；感知机模型 f(x)=\operatorname{sign}\left(\sum_{j=1}^{N} \alpha_{j} y_{j} x_{j} \cdot x+b\right)，其中， \alpha = (\alpha_1, \alpha_2, \cdots, \alpha_N)^T$。

$(1)\alpha \leftarrow 0,b\leftarrow 0$$(1) \; \alpha \leftarrow 0, b \leftarrow 0$

$(2)\text{在}\text{训}\text{练}\text{集}\text{中}\text{选}\text{取}\text{数}\text{据}（x_i,y_i）$$(2) \; 在训练集中选取数据（x_i,y_i）$

$(3)\text{如}\text{果}{y}_i(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b)\le 0:$$(3) \; 如果 \; y_i \left(\sum_{j=1}^{N} \alpha_{j} y_{j} x_{j} \cdot x+b\right) \leq 0 \; :$

$\begin{array}{c}{\alpha }_i\leftarrow {\alpha }_i+\eta \\ b\leftarrow b+\eta y_i\end{array}$$\alpha_{i} \leftarrow \alpha_{i}+\eta \\ b \leftarrow b+\eta y_{i}$

$(4)\text{转}\text{至}(2)，\text{直}\text{至}\text{训}\text{练}\text{集}\text{中}\text{没}\text{有}\text{误}\text{分}\text{类}\text{点}$$(4) \; 转至(2)，直至训练集中没有误分类点$

对偶形式中训练实例仅以内积的形式出现。为了方便，可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储，该矩阵称为Gram矩阵：