条件随机场2021-09-26
条件随机场概述
条件随机场(conditional random field, CRF)是一种条件概率分布模型,其特点是假设输出随机变量构成马尔可夫随机场。对于线性链条件随机场,其问题变成了由输入序列对输出序列预测的判别模型,形式为对数线性模型,学习方法通常是极大似然估计或正则化的极大似然估计。
概率无向图模型
概率无向图模型,又称为马尔可夫随机场,是一个可以由无向图表示的联合概率分布。
基本概念
图是由结点及连接结点的边组成的集合。结点和边分别记作和,结点和边的集合分别记作和,图记作。无向图是指边没有方向的图。
概率图模型是由图表示的概率分布。设有联合概率分布,是一组随机变量。概率分布由无向图表示,即在图中,结点表示一个随机变量,;边表示随机变量之间的概率依赖关系。
三种马尔可夫性
给定一个联合概率分布和表示该模型的无向图。对无向图表示的随机变量之间存在的马尔可夫性进行定义,马尔可夫性包括成对马尔可夫性、局部马尔可夫性、全局马尔可夫性,并且,这三种独立性是等价的。
- 成对马尔可夫性
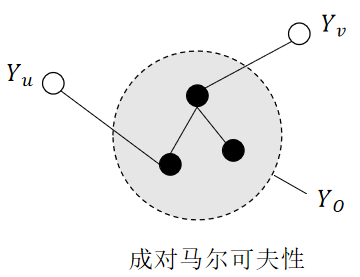
设和是无向图中任意两个没有边连接的结点,结点和分别对应随机变量和。其它所有结点为,对应的随机变量组是。成对马尔可夫性是指给定随机变量组的条件下随机变量和是条件独立的,即:
- 局部马尔可夫性
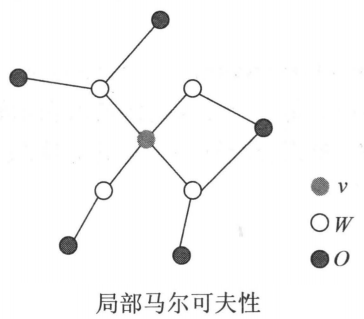
设是无向图中任意一个结点,是与有边连接所有结点,是和以外的其它所有结点。表示的随机变量是,表示的随机变量组是,表示的随机变量组是。局部马尔可夫性是指给定随机变量组的条件下随机变量与随机变量组是独立的,即:
在时,等价地:
该公式可以概括为:
其中,表示所有与连接的点,表示除了以外的其它点 - 全局马尔可夫性
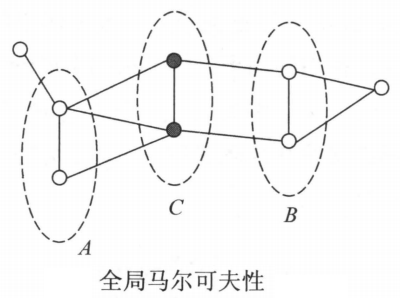
设结点集合,是在无向图中被结点集合分开的任意结点集合。结点集合,和所对应的随机变量组分别是,和。全局马尔可夫性是指给定随机变量组条件下随机变量组和是条件独立的,即
概率无向图模型定义
定义:概率无向图模型 设有联合概率分布,由无向图表示,在图中,结点表示随机变量,边表示随机变量之间的依赖关系。如果联合概率分布满足成对、局部或全局马尔可夫性,就称此联合概率分布为概率无向图模型,或马尔可夫随机场。
简记:概率无向图模型是,可以由无向图表示,且无向图结点间的概率满足马尔可夫性。
概率无向图模型的因子分解
定义:团与最大团 无向图中任何两个结点均有连接的结点子集称为团。若是无向图中的一个团,并且不能再加进任何一个的结点使其称为一个更大的团,则称此为最大团。
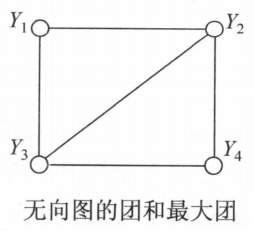
如上图所示的无向图,最大团为:和。
定理:定理 概率无向图模型的联合概率分布可以表示为如下形式:
其中,是无向图的最大团,是中的结点对应的随机变量,是上定义的严格正函数,乘积是在无向图所有的最大团上进行的。 上述定理表明,概率无向图模型的联合概率分布可以表示为其最大团上的随机变量的函数的乘积形式。
条件随机场表示
条件随机场定义
条件随机场(conditional random field)是给定随机变量条件下,随机变量的马尔可夫随机场。
定义:条件随机场 设和是随机变量,是给定的条件下的条件概率分布。若随机变量构成一个由无向图表示的马尔可夫随机场,即:
对任意结点成立,则称条件概率分布为条件随机场。式中表示在图中与结点有边连接的所有结点,表示结点以外的所有结点,、、为结点、、对应的随机变量。
注意:在定义中并没有要求和具有相同的结构。
线性链条件随机场定义
现实中,一般假设条件随机场中和具有相同结构。现假设无向图为下图所示的线性链的情况,即图的定义为:
在此情况下,,最大团是相邻两个结点的集合。
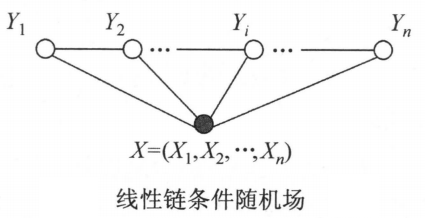
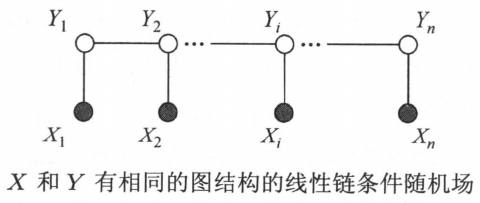
线性链条件随机场可以用于标注等问题。这时,在条件概率模型中,是输出变量,表示预测出的标记序列,是输入变量,表示需要标注的观测序列。例如,我爱中国,名词,动词,名词。
定义:线性链条件随机场 设均为线性表示的随机变量序列,若在给定随机变量序列的条件下,随机变量序列的条件概率分布构成条件随机场,即满足马尔可夫性:
在和时只考虑单边 则称为线性链条件随机场。在标注问题中,表示输入观测序列,表示对应的输出标记序列或状态序列。
条件随机场的参数化形式
根据定理,可以给出线性链条件随机场的因子分解式,各因子是定义在相邻两个结点(最大团)上的势函数。
定理:线性链条件随机场的参数化形式 设为线性链条件随机场,则在随机变量取值为的条件下,随机变量取值为的条件概率具有如下形式:
其中,是定义在边上的特征函数,称为转移特征;是定义在结点上的特征函数,称为状态特征;和都依赖于位置,是局部特征函数,通常取值为或;和是对应的权值;是规范化因子,求和是在所有可能的输出序列上进行的。 条件随机场的简化形式
在条件随机场的参数化形式中,同一特征在各个位置都有定义,可以对同一个特征在各个位置求和,将局部特征函数转化为一个全局特征函数,这样就可以将条件随机场写成权值向量和特征向量的内积的形式,即条件随机场的简化形式。
首先,将转移特征和状态特征及其权值用统一的符号表示。
设有个转移特征,个状态特征,,记:
然后,对转移和状态特征在各个位置求和,得到全局特征函数,记作:
用表示特征的权值,得到全局特征权值,即:
于是,条件随机场可表示为:
若以表示全局特征向量,即:
以表示权值向量,即:
那么,条件随机场可以写成向量与的内积的形式:
条件随机场的矩阵形式
条件随机场还可以由矩阵表示。假设是由式给出的线性链条件随机场,表示对给定观测序列,相应的标记序列的条件概率。
对每个标记序列引进特殊的起点和终点状态标记和,这时标注序列的概率可以通过矩阵形式表示并有效计算。
对观测序列的每一个位置,由于和在个标记中取值,可以定义一个阶矩阵随机变量:
矩阵随机变量的元素为:
其中,和分别由式和式给出,和是标记随机变量和的取值。 这样,给定观测序列,相应标记序列的非规范化概率可以通过该序列个矩阵的适当元素的乘积表示。因此,条件概率为:
其中, 可以看到,矩阵形式展开后与参数化形式或简化形式是一致的。
条件随机场概率计算问题
前向-后向算法
前向向量
对每个指标,定义前向向量:
否则 递推公式为:
其中, 又可表示为:
表示在位置的标记是并且从1到的前部分标记序列的非规范化概率,可取的值有个,所以是维列向量。
后向向量
对每个指标,定义后向向量:
否则 递推公式为:
又可表示为:
表示在位置的标记为并且从到的后部分标记序列的非规范化概率。
概率计算
根据前向-后向向量的定义,可以得出如下概率:
其中,是元素均为的维列向量 期望值的计算
利用前向-后向向量,可以计算特征函数关于联合分布和条件分布的数学期望。
特征函数关于条件分布的数学期望
其中, 特征函数关于联合分布的数学期望
假设经验分布为,那么特征函数关于联合分布的数学期望为:
其中,
条件随机场的学习算法
改进的迭代尺度法
已知训练数据集,由此可知经验概率分布。可以通过极大化训练数据的对数似然函数来求模型参数。
训练数据的对数似然函数为:
当是一个由式给出的条件随机场模型时,对数似然函数为:
改进的迭代尺度法通过迭代的方法不断优化对数似然函数改变量的下界,达到极大化似然函数的目的。
假设模型的当前参数向量为,向量的增量为,更新参数向量为。在每步迭代过程中,改进的迭代尺度法通过依次求解式和式,得到。
关于转移特征的更新方程
其中, 关于状态特征的更新方程
其中, 这里,是在数据中出现所有特征数的总和:
算法条件随机场模型学习的改进的迭代尺度法
输入:特征函数,;经验分布
输出:参数估计值;模型
对所有,初始化
对每一:
当时,令是如下方程的解:
。
解得:其中, 当时,令是如下方程的解:
解得:其中, 更新的值:
如果不是所有都收敛,重复步骤
在式中,表示数据中的特征总数,对不同的数据取值可能不同。为了处理该问题,定义松弛特征:
式中是一个常数。选择足够大的常数使得对训练数据集的所有数据,成立。此时特征总数可取。
拟牛顿法
条件随机场的对数似然函数为:
将条件随机场的简化形式带入得:
令,则最大化等价于最小化,所以,优化目标函数为:
的梯度函数是:
算法条件随机场模型学习的算法
输入:特征函数;经验分布
输出:最优参数值;最优模型
选定初始点,取为正定对称矩阵,置
计算。若,则停止计算,否则转
由求出
一维搜索:求使得:
置
计算,若,则停止计算;否则,按下式求出
其中,
置,转
条件随机场的预测算法
已知:
根据条件随机场的矩阵形式,可得:
于是,条件随机场的预测问题成为求非规范化概率最大的最优路径问题:
根据定义可以推导:
其中,
因此,优化目标可以写成如下形式:
其中,
算法条件随机场的维特比算法
输入:模型特征向量;权值向量;观测序列
输出:最优路径
初始化
递推:对
终止
返回路径
求得最优路径:
参考文档
- 《统计学习方法》啃书手册|第11章 条件随机场 - 知乎 (zhihu.com)
- 一文读懂机器学习概率图模型(附示例和学习资源) - 云+社区 - 腾讯云 (tencent.com)





