Voting

针对分类问题，多个模型投票，少数服从多数，得到最终的预测结果。

选择模型时，要求模型是弱相关性的。

Averaging

针对回归问题，多个模型求（加权）均值，模型系数可以通过网格搜索获取。

Stacking与Blending

二者本质相同，混叫。

整体架构如下：

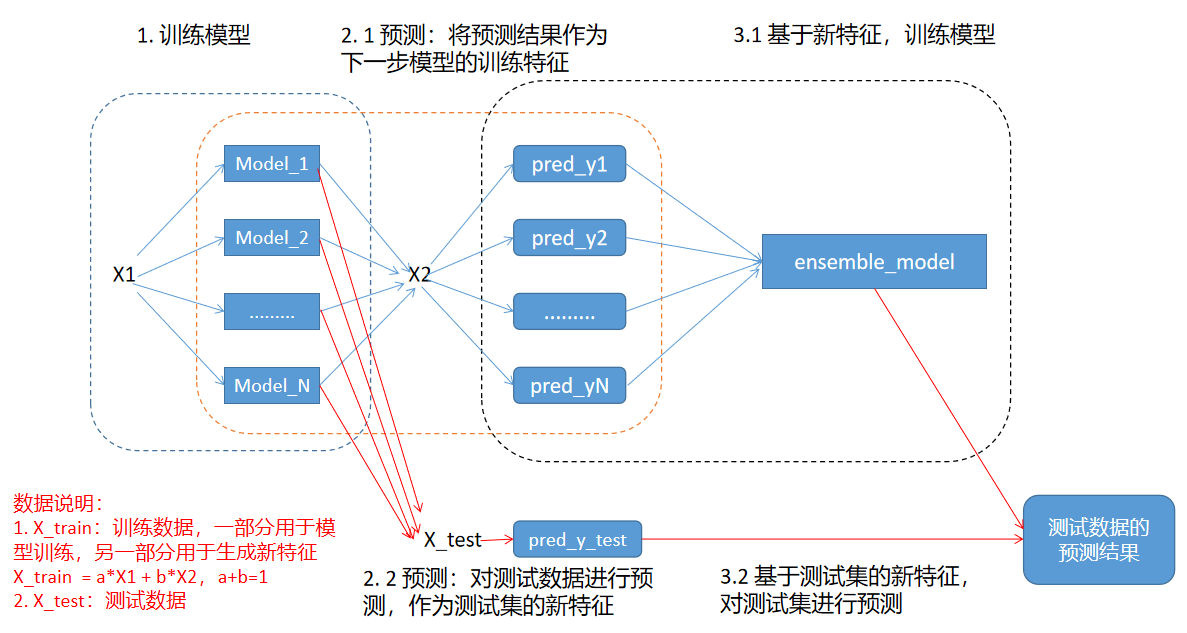
Stacking

其本质是使用模型对数据特征进行编码，从而得到新的特征，基于新特征，再训练模型进行最终预测。

1. 生成新特征

   对训练数据，使用交叉验证训练模型，每一折都将得到预测结果，将所有预测结果合并起来，即为整个训练数据集的预测结果。对该预测结果，换一个角度，可以看成是新的特征数据。假设有$n$$n$条训练数据，则经过一次模型训练，可以得到$n\times 1$$n \times 1$的新特征数据（预测结果）。如果经过$m$$m$个模型，则可以得到$n\times m$$n \times m$的新特征数据。

   对测试数据，每一折都会对全量数据进行预测，可以采用取平均的方式得到对应的全量测试数据的预测结果。

   下图为1个模型得到的新特征数据：

   

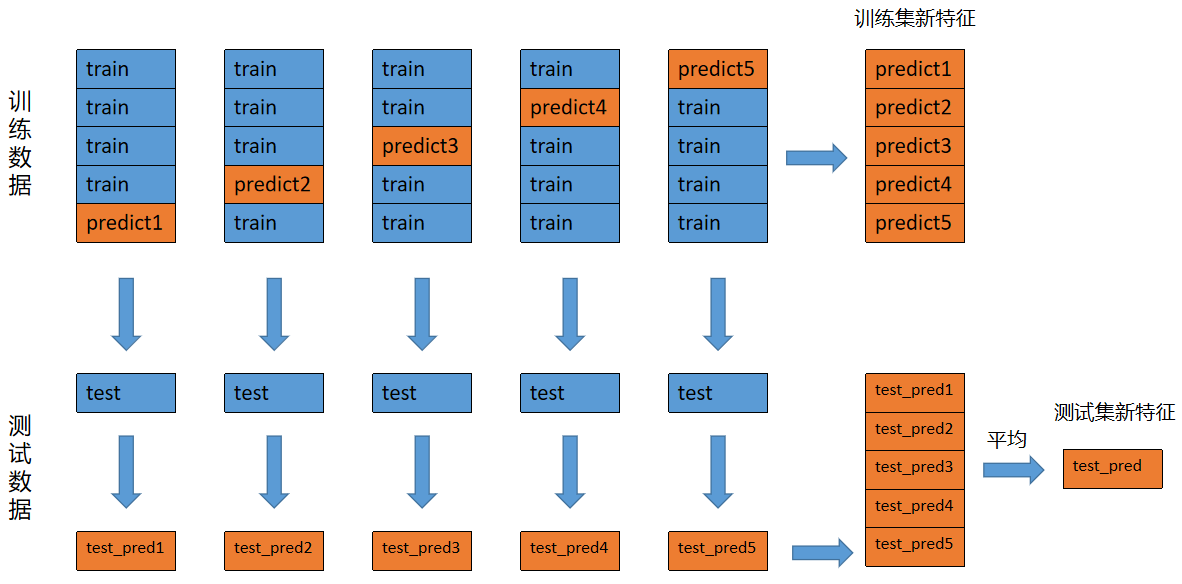
2. 预测

基于新的特征，训练新的模型，然后对新测试数据特征进行预测，得到最终的预测结果。

下图展示的是整体Stacking过程：经过LR、RF、GBDT共3个模型生成新特征数据，然后再训练XGB模型并进行预测。

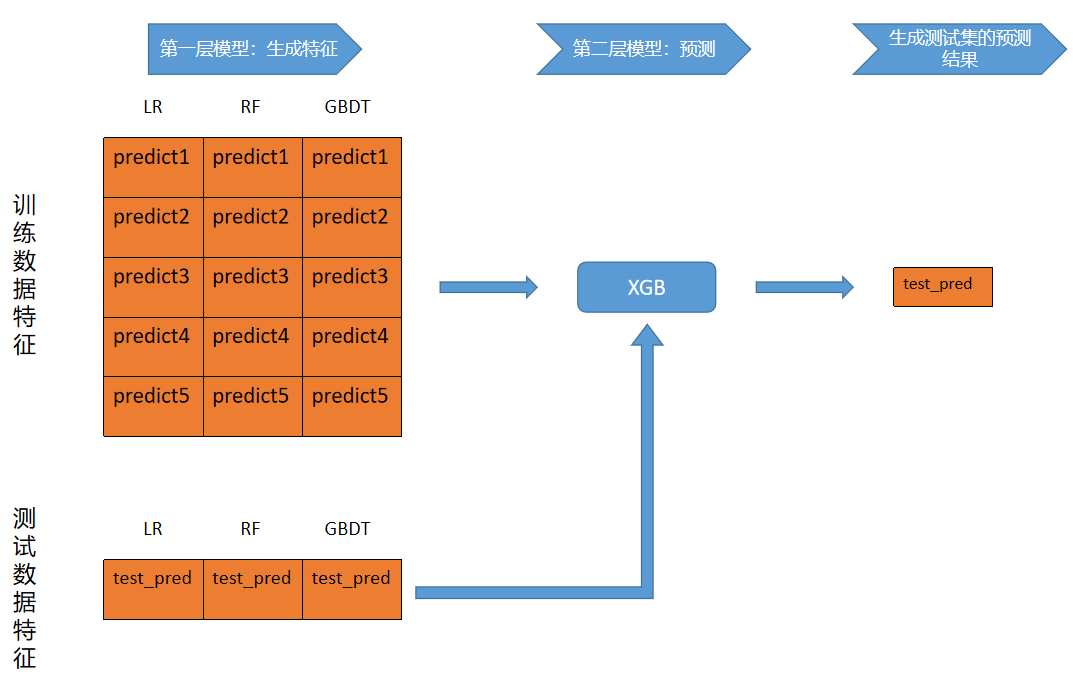
Blending

非交叉堆叠。整体做法和Stacking类似，不同之处是Blending不做交叉验证，在第一层模型训练时，将训练数据按照一定比例切分，比如7:3，70%的数据用作训练，30%的数据用作验证，然后将验证结果作为第二层模型的训练特征。

AdaBoost

由 Yoav Freund 和 Robert Schapire 提出，两人因此获得了哥德尔奖。

基本原理

模型集成的一种宏方法，目的是将若干个弱学习器组合为一个强学习器，核心是如何计算样本权重和学习器权重：

1. 串行训练弱学习器；

2. 权重调整

   • 调整弱学习器权重：根据弱学习的分类误差率调整该学习器的权重；
   • 调整样本权重：每一轮训练完成后，根据当前弱学习器的分类结果调整样本的权重，即训练正确的样本降低权重，训练错误的样本提高权重；

3. 将若学习器组合为强学习器。

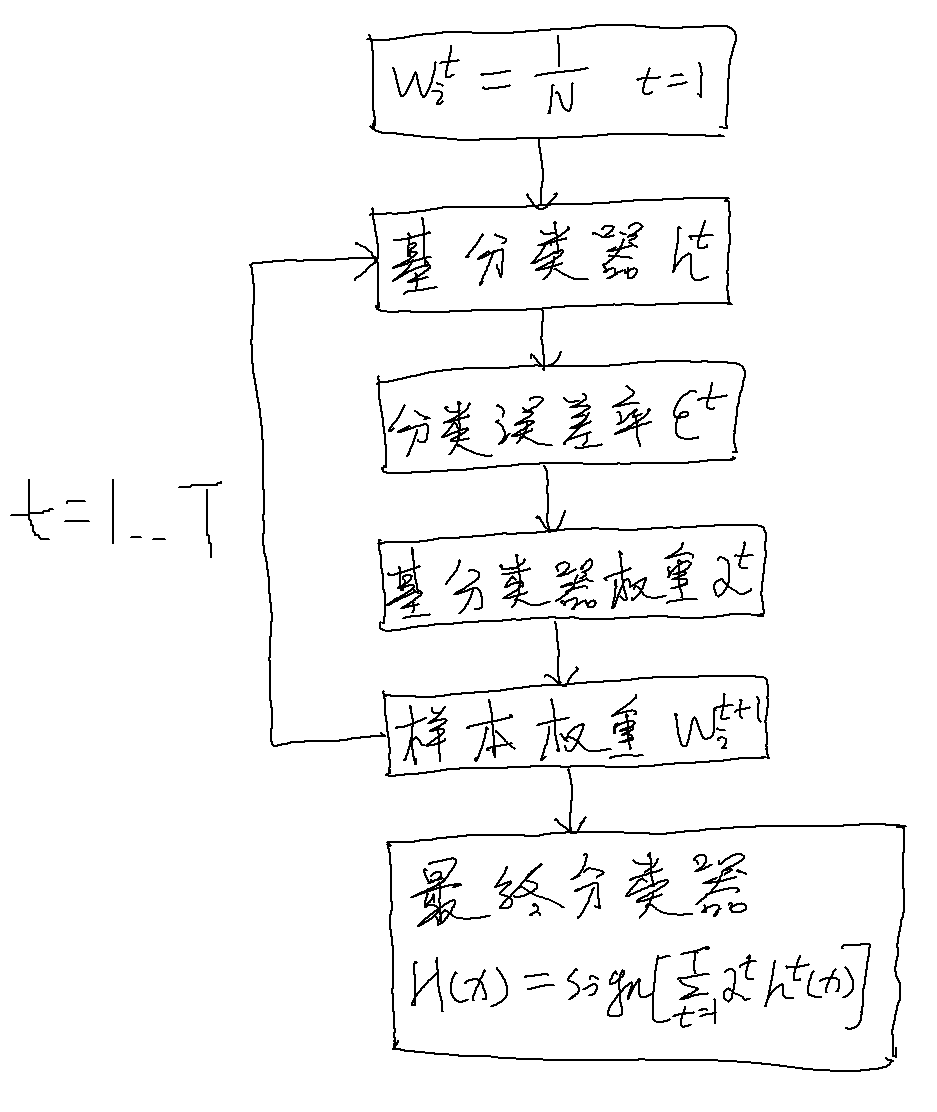
实现步骤

首先，定义如下符号：

1. $h^t$$h^t$：第$t$$t$轮的弱学习器，其中，$1\le t\le T$$1 \le t \le T$

2. ${\alpha }^t$$\alpha ^t$：第$t$$t$轮弱学习器的权重

3. $w_i^t$$w_i ^t$：第$t$$t$轮时，第$i$$i$个样本的权重，其中，$1\le i\le N$$1 \le i \le N$

4. $y_i$$y_i$：第$i$$i$个样本的真实值

5. ${\epsilon }^t$$\varepsilon ^t$：第$t$$t$轮的分类误差率

6. $I(y\ne \hat{y})$$I(y \neq \hat{y})$：指示函数，表示当$y$$y$不等于$\hat{y}$$\hat{y}$时为1，否则为0

7. $\mathbf{sign}(x)$$\mathbf{sign}(x)$：指示函数

   $$\begin{array}{}\text{(1)}& \begin{array}{c}\mathbf{sign}(x)=\{\begin{array}{c}1x>0\\ 0x=0\\ -1x<0\end{array}\end{array}\end{array}$$

下图为AdaBoost的过程图例（分类问题）：

接下来，以二分类问题($y\in (1,-1)$$y \in (1, -1)$)为例，开始AdaBoost的训练过程：

1. 初始化训练数据的权值分布

   $W^t=(w_1^t,w_2^t,\cdots ,w_N^t)$$W^t = (w^t_1,w^t_2, \cdots, w^t_N)$，其中，$t=1$$t=1$

2. 对$t=1,2,\cdots ,T$$t=1,2,\cdots,T$

   • 基于当前的权值分布$W^t$$W^t$，训练基分类器：$h^t$$h^t$

   • 计算$h^t(x)$$h^t(x)$在训练数据上的分类误差率

     $$\begin{array}{}\text{(2)}& {\epsilon }^t=\sum _{i=1}^{N}P(h^t(x)\ne y_i)=\sum _{i=1}^N{w}_i^{t}I(h^t(x_i)\ne y_i)=\sum _{i\in err}{w}_i^t\end{array}$$

     由上式可知，分类误差率等于预测错误样本的权重。

   • 计算若学习器$h^t$$h^t$的权重

     $$\begin{array}{}\text{(3)}& {\alpha }^t=\frac{1}{2}\ln \frac{1-{\epsilon }^t}{{\epsilon }^t}\end{array}$$

   • 更新训练数据的权值分布

     $$\begin{array}{}\text{(4)}& \begin{array}{c}{w}_i^{t+1}=\frac{w_i^t}{Z^t}{e}^{-{\alpha }^t{y}_i{h}^t(x_i)}\\ Z^t=\sum _{i=1}^N{w}_i^t{e}^{-{\alpha }^t{y}_i{h}^t(x_i)}\end{array}\end{array}$$

3. 构建弱分类器的线性组合

   $$\begin{array}{}\text{(5)}& f(x)=\sum _{t=1}^T{\alpha }^t{h}^t(x)\end{array}$$

   得到最终的分类器：

   $$\begin{array}{}\text{(6)}& H(x)=\mathbf{sign}(f(x))\end{array}$$

公式简化

1. 简化归一化因子$Z^t$$Z^t$

   $$\begin{array}{}\text{(7)}& \begin{array}{rl}{Z}^t& =\sum _{i=1}^N{w}_i^t{e}^{-{\alpha }^t{y}_i{h}^t(x_i)}\\ & =\sum _{i\in corr}{w}_i^t{e}^{-{\alpha }^t}+\sum _{i\in err}{w}_i^t{e}^{{\alpha }^t}\\ & =(1-{\epsilon }^t)e^{-{\alpha }^t}+{\epsilon }^t{e}^{{\alpha }^t}\\ & =(1-{\epsilon }^t)\sqrt[2]{\frac{{\epsilon }^t}{1-{\epsilon }^t}}+{\epsilon }^t\sqrt[2]{\frac{1-{\epsilon }^t}{{\epsilon }^t}}\\ & =2\sqrt[2]{{\epsilon }^t(1-{\epsilon }^t)}\end{array}\end{array}$$

2. 简化样本权重

   $$\begin{array}{}\text{(8)}& \begin{array}{rl}{w}_i^{t+1}& =\frac{w_i^t}{Z^t}{e}^{-{\alpha }^t{y}_i{h}^t(x_i)}\\ & =\{\begin{array}{c}\frac{w_i^t}{Z^t}{e}^{-{\alpha }^t}{y}_i=h^t(x_i)\\ \frac{w_i^t}{Z^t}{e}^{{\alpha }^t}{y}_i\ne h^t(x_i)\end{array}\\ & =\{\begin{array}{c}\frac{w_i^t}{Z^t}\sqrt[2]{\frac{{\epsilon }^t}{1-{\epsilon }^t}}{y}_i=h^t(x_i)\\ \frac{w_i^t}{Z^t}\sqrt[2]{\frac{1-{\epsilon }^t}{{\epsilon }^t}}{y}_i\ne h^t(x_i)\end{array}\\ & =\{\begin{array}{c}\frac{w_i^t}{2(1-{\epsilon }^t)}{y}_i=h^t(x_i)\\ \frac{w_i^t}{2{\epsilon }^t}{y}_i\ne h^t(x_i)\end{array}\end{array}\end{array}$$

3. 有意思的事情

   对于预测正确的样本，其更新后的样本权重之和为0.5：

   $$\begin{array}{}\text{(9)}& \begin{array}{rl}\sum _{i\in corr}\frac{w_i^t}{2(1-{\epsilon }^t)}& =\frac{1}{2(1-{\epsilon }^t)}\sum _{i\in corr}{w}_i^t\\ & =\frac{1}{2(1-{\epsilon }^t)}(1-{\epsilon }^t)\\ & =\frac{1}{2}\end{array}\end{array}$$

   对于预测错误的样本，结论一样。