基本原理

降维原理：组间方差大、组内方差小。

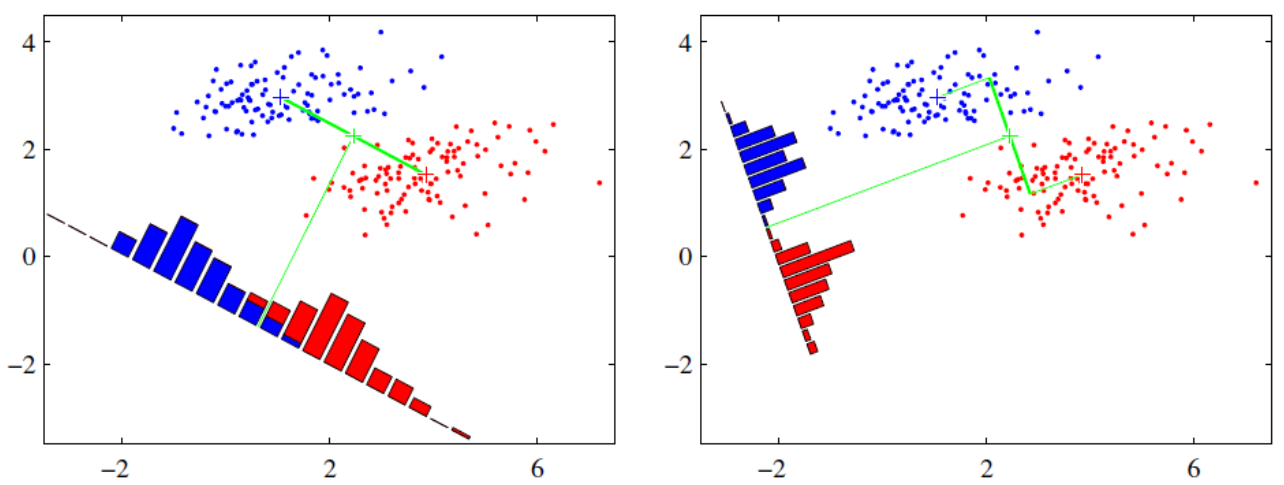
降维步骤

以二类数据为例对降维过程进行说明。首先，定义如下变量：

1. 数据集：${\mathbf{x}}^{(i)}=[x_1^{(i)},x_2^{(i)},\cdots ,x_d^{(i)}{]}^{\mathrm{T}}$$\mathbf{x}^{(i)} = [x_1^{(i)},x_2^{(i)},\cdots,x_d^{(i)} ]^{\mathrm{T}}$，共$N$$N$个样本
2. 类别：$c=\{c_1,c_2\}$$c=\{c_1,c_2 \}$，其中，$c_1$$c_1$样本个数为$N_1$$N_1$，$c_2$$c_2$样本个数为$N_2$$N_2$，$N=N_1+N_2$$N=N_1+N_2$

原始数据为$d$$d$维，在"组间方差大、组内方差小"的原则下，先降1维；

1. 投影

   使用向量$\mathbf{w}=[w_1,w_2,\cdots ,w_d{]}^{\mathrm{T}}$$\mathbf{w} = [w_1,w_2,\cdots,w_d]^{\mathrm{T}}$对数据进行投影，并得到投影后的结果：

   $$\begin{array}{}\text{(1)}& y={\mathbf{w}}^{\mathrm{T}}\mathbf{x}\end{array}$$

2. 计算原始数据类内均值

   $$\begin{array}{}\text{(2)}& \begin{array}{c}\mu {\mu }_i=\frac{1}{N_i}\sum _{\mathbf{x}\in c_i}\mathbf{x}\\ \text{其}\text{中}，i=\{1,2\}，\mu {\mu }_i\text{的}\text{维}\text{度}\text{是}d\times 1\end{array}\end{array}$$

3. 计算投影后的样本点均值

   $$\begin{array}{}\text{(3)}& {\tilde{\mu }}_i=\frac{1}{N_i}\sum _{y\in c_i}y=\frac{1}{N_i}\sum _{y\in c_i}{\mathbf{w}}^{\mathrm{T}}x={\mathbf{w}}^{\mathrm{T}}\mu {\mu }_i\end{array}$$

   由此可知，投影后的均值是样本中心点的投影。

4. 定义投影后数据的方差：度量组内差异

   $$\begin{array}{}\text{(4)}& \begin{array}{rl}{\tilde{s}}_i^2& =\sum _{y\in c_i}{(y-{\tilde{\mu }}_i)}^2\\ & =\sum _{\mathbf{x}\in c_i}{({\mathbf{w}}^{\mathrm{T}}\mathbf{x}-{\mathbf{w}}^{\mathrm{T}}\mu {\mu }_i)}^2\\ & =\sum _{\mathbf{x}\in c_i}{\mathbf{w}}^{\mathrm{T}}(\mathbf{x}-\mu {\mu }_i){(\mathbf{x}-\mu {\mu }_i)}^{\mathrm{T}}\mathbf{w}\end{array}\end{array}$$

   ${\tilde{s}}_i^2$$\tilde{s}_{i}^{2}$的几何意义是反映了样本点的密集程度，值越大，投影后数据越分散，反之，越集中。

   为方便后续计算，定义中间部分为：

   $$\begin{array}{}\text{(5)}& \begin{array}{c}{S}_i=\sum _{\mathbf{x}\in c_i}(\mathbf{x}-\mu {\mu }_i){(\mathbf{x}-\mu {\mu }_i)}^{\mathrm{T}}\\ \text{注}：S_i\text{的}\text{维}\text{度}\text{是}d\times d\end{array}\end{array}$$

   这也被称为散列矩阵（scatter matrices）。

   定义$S_W$$S_W$（Within-class scatter matrix）为：

   $$\begin{gathered} \begin{array}{}\text{(6)}& S_W=S_1+S_2\end{array} \\ \text{注}：S_W\text{的}\text{维}\text{度}\text{是}d\times d \end{gathered}$$

    

5. 定义投影后组间均值差异：度量组间差异

   $$\begin{array}{}\text{(7)}& \begin{array}{rl}A& =({\tilde{\mu }}_1-{\tilde{\mu }}_2{)}^2\\ & =({\mathbf{w}}^{\mathrm{T}}\mu {\mu }_1-{\mathbf{w}}^{\mathrm{T}}\mu {\mu }_2)({\mathbf{w}}^{\mathrm{T}}\mu {\mu }_1-{\mathbf{w}}^{\mathrm{T}}\mu {\mu }_2{)}^{\mathbf{T}}\\ & ={\mathbf{w}}^{\mathrm{T}}(\mu {\mu }_1-\mu {\mu }_2)(\mu {\mu }_1-\mu {\mu }_2{)}^{\mathbf{T}}\mathbf{w}\end{array}\end{array}$$

   定义$S_B$$S_B$称为（Between-class scatter matrix）：

   $$\begin{array}{}\text{(8)}& \begin{array}{c}{S}_B=(\mu {\mu }_1-\mu {\mu }_2)(\mu {\mu }_1-\mu {\mu }_2{)}^{\mathbf{T}}\\ \text{注}：S_B\text{的}\text{维}\text{度}\text{是}d\times d\end{array}\end{array}$$

6. 定义最终度量公式

   $$\begin{array}{}\text{(9)}& \begin{array}{rl}J(w)& =\frac{{({\tilde{\mu }}_1-{\tilde{\mu }}_2)}^2}{{\tilde{s}}_1^2+{\tilde{s}}_2^2}\\ & =\frac{{\mathbf{w}}^{\mathbf{T}}{S}_B\mathbf{w}}{{\mathbf{w}}^{\mathbf{T}}{S}_W\mathbf{w}}\end{array}\end{array}$$

7. 定义优化目标

   $$\begin{array}{}\text{(10)}& \begin{array}{c}maxJ(\mathbf{w})\\ s.t.\Vert {\mathbf{w}}^{\mathbf{T}}{S}_W\mathbf{w}\Vert =1\end{array}\end{array}$$

   增加约束$\Vert {\mathbf{w}}^{\mathbf{T}}{S}_W\mathbf{w}\Vert =1$$\left\|\mathbf{w}^{\mathbf{T}} S_{W} \mathbf{w}\right\|=1$的原因：因为不做归一化的话，$\mathbf{w}$$\mathbf{w}$扩大任何倍，公式都成立，因此无法确定$\mathbf{w}$$\mathbf{w}$。

8. 定义拉格朗日函数

   $$\begin{array}{}\text{(11)}& \mathcal{L}(\mathbf{w},\lambda )={\mathbf{w}}^{\mathbf{T}}{S}_B\mathbf{w}-\lambda ({\mathbf{w}}^{\mathbf{T}}{S}_W\mathbf{w}-1)\end{array}$$

   求导得：

   $$\begin{array}{}\text{(12)}& \begin{array}{rl}\frac{\partial \mathcal{L}}{\partial \mathbf{w}}& =S_B\mathbf{w}+S_B^T\mathbf{w}-\lambda S_W\mathbf{w}-\lambda S_W^T\mathbf{w}\\ & =2S_B\mathbf{w}-2\lambda S_W\mathbf{w}(\text{因}\text{为}{S}_B\text{和}{S}_W\text{为}\text{对}\text{称}\text{矩}\text{阵})\\ & =0\end{array}\end{array}$$

   解得：

   $$\begin{gathered} \begin{array}{}\text{(13)}& S_B\mathbf{w}=\lambda S_W\mathbf{w} \\ {S}_W^{-1}{S}_B\mathbf{w}=\lambda \mathbf{w}\end{array} \end{gathered}$$

   可见，$\mathbf{w}$$\mathbf{w}$是矩阵$S_W^{-1}{S}_B$$S_{W}^{-1} S_{B}$的特征向量，当前可以取最大特征值对应的特征向量。

    

    

   因为：

   $$\begin{array}{}\text{(14)}& S_B\mathbf{w}=(\mu {\mu }_1-\mu {\mu }_2)(\mu {\mu }_1-\mu {\mu }_2{)}^{\mathbf{T}}\mathbf{w}\end{array}$$

   而$(\mu {\mu }_1-\mu {\mu }_2{)}^{\mathbf{T}}\mathbf{w}$$(\pmb{\mu}_{1} - \pmb{\mu}_{2})^{\mathbf{T}} \mathbf{w}$为一个数值，假设$(\mu {\mu }_1-\mu {\mu }_2{)}^{\mathbf{T}}\mathbf{w}=\alpha$$(\pmb{\mu}_{1} - \pmb{\mu}_{2})^{\mathbf{T}} \mathbf{w}=\alpha$，那么总可以对$\mathbf{w}$$\mathbf{w}$进行缩放，使得$\alpha =\lambda$$\alpha = \lambda$，即：

   $$\begin{array}{}\text{(15)}& S_B\mathbf{w}=(\mu {\mu }_1-\mu {\mu }_2)(\mu {\mu }_1-\mu {\mu }_2{)}^{\mathbf{T}}\mathbf{w}=(\mu {\mu }_1-\mu {\mu }_2)\lambda \end{array}$$

   那么：

   $$\begin{array}{}\text{(16)}& S_W^{-1}{S}_B\mathbf{w}=S_W^{-1}(\mu {\mu }_1-\mu {\mu }_2)\lambda =\lambda \mathbf{w}\end{array}$$

   所以：

   $$\begin{array}{}\text{(17)}& \mathbf{w}=S_W^{-1}(\mu {\mu }_1-\mu {\mu }_2)\end{array}$$

   至此，只需要求出原始样本的均值和方差就可以求出最佳的方向$\mathbf{w}$$\mathbf{w}$。

参考链接

1. 线性判别分析LDA原理总结 - 刘建平Pinard - 博客园 (cnblogs.com)
2. 为什么线性判别分析的降维维数不能大于类别数减一？ - 知乎 (zhihu.com)
3. Dimensionality Reduction——LDA线性判别分析原理篇 - 知乎 (zhihu.com)
4. Linear Discriminant Analysis (sebastianraschka.com)