Ridge和Lasso2023-02-20
线性回归
模型定义
多元线性回归模型定义如下:
令矩阵为:
损失函数为:
求
一阶偏导数为:
在Hessian矩阵为正定矩阵的假设下,令一阶偏导数为0,可得:
因此,只要可逆,即可通过数值计算的方式直接求得最优参数。
但是,如果不可逆,如何处理?
从不可逆到可逆
因为是对称矩阵,根据对称矩阵的性质:
因此:
其中, 由于是半正定矩阵,所以,中的元素(特征值)大于等于0。而的元素都大于0,因此,两者的和一定大于0。
这意味着,对矩阵而言,其特征值(奇异值)都大于0,因此该矩阵一定可逆。
当较小时,可以相信,在数值解中加上,对最终结果影响不大。
那么,修正后的数值解:
虽然,到底取多少还不确定,但该数值解理论上保证是可求解的。
对于搞数学推导的同学,可以休息了。但是,对于做机器学习的同学,还应该思考,这意味着什么?或者,有哪些启发?
Ridge
数值解带来的启发
已知了数值解,能不能反推,应该将损失函数做哪些修改呢?
此时,从上帝视角,如果定义损失函数:
损失函数对参数求偏导,可得:
令导数为0:
解上式,可得:
该数值解,和原始数值解修正后的结果一致。该过程相当于,给定了答案,猜到了问题。
定义Ridge回归
定义新损失函数:
基于该损失函数求解参数的过程,称作Ridge回归。
等高线
重新认识损失函数。
如果将损失函数从拉格朗日函数的角度去看,则发现:
等价于 因此,可以从不等式角度重新审视损失函数:
其中,为关于的某个函数 假设有两个未知变量,对该不等式做等高线,如下图:
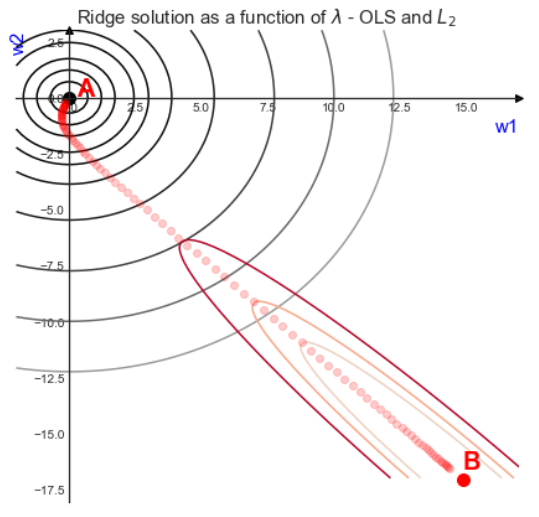
其中,红色曲线为的等高线,黑色线为的等高线。最优解在点和点之间的轨迹中间:
- 趋于0:最优解趋于点,如果等于0,相当于没有加入正则项,最优解为点
- 趋于正无穷:最优解趋于点,如果等于正无穷,最优解为点,即所有参数为0
从上图还可以看出,当存在约束的时候,L2正则会倾向同时将参数压小。
Lasso
定义Lasso回归
Lasso对应的损失函数:
等高线
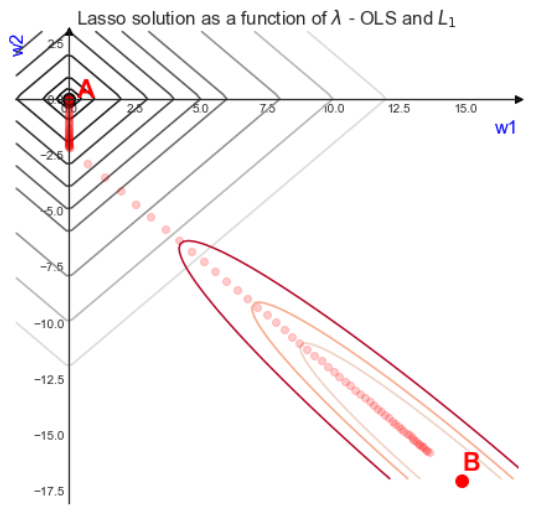
同Ridge,最优解在点和点之间的轨迹中间:
- 趋于0:最优解趋于点,如果等于0,相当于没有加入正则项,最优解为点
- 趋于正无穷:最优解趋于点,如果等于正无穷,最优解为点,即所有参数为0
同Ridge不同的是,从点出发,有一段轨迹在坐标轴上,此时,的的权重将为0。因此,Lasso可能会将某个维度参数权重压缩为0,也就是所谓的:L1正则化可以做特征选择。
附录
的结果是半正定矩阵
反证法。
设存在负特征值,该特征值对应的特征向量为。那么:
左右同乘以:
对上式整理得:
左侧:
右侧:是向量自身的模长的平方,而且是特征向量,所以非零,所以,而,因此,
左右矛盾,故假设不成立。
因此,是半正定矩阵。
方阵对角化
其中,为方阵的特征值组成的方阵,为特征值对应的特征向量组成的方阵
对称矩阵性质
设,同时,。
- 特征向量正交:

