名词术语

1. 凸聚类：若聚类结果中每个簇都是一个凸包（包含簇中所有样本的凸多面体），且凸包不相交，这称该数据集是凸数据集，该聚类算法是凸聚类；反之，称为非凸聚类。

2. 原型聚类：输出线性分类边界的聚类算法显然都是凸聚类，这样的算法有：K均值，LVQ；而曲线分类边界的也显然是非凸聚类，高斯混合聚类，在簇间方差不同时，其决策边界为弧线，所以高混合聚类为非凸聚类。

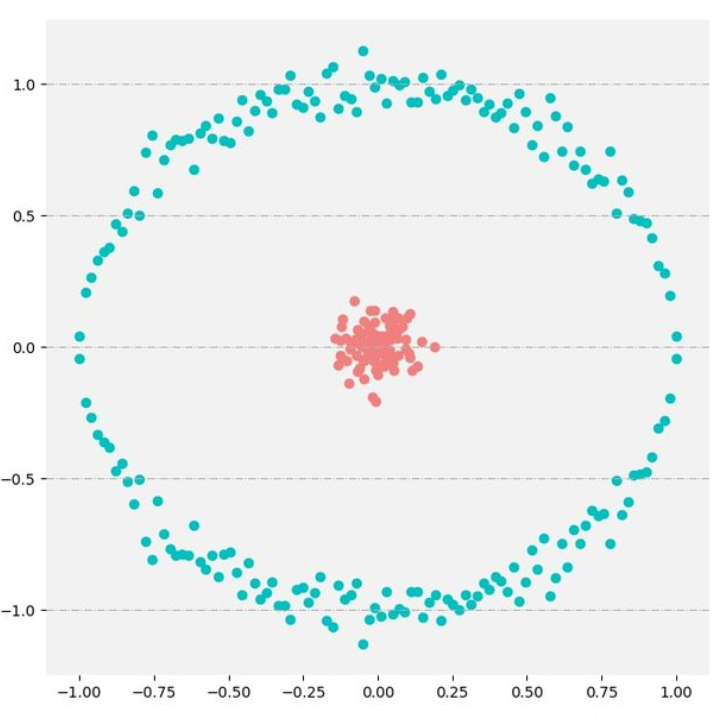
3. 密度聚类：DBSCAN，如下图情况，显然当领域参数符合一定条件时，会生成两个簇，其中外簇会包括内簇，所以DBSCAN显然也是非凸聚类。

   

距离

闵科夫斯基距离

缺点：对高维数据聚类时通常无效，因为样本之间的距离随着维数的增加而增加。

欧式距离(P=2)

曼哈顿距离(P=1)

切比雪夫距离

当$p\to \mathrm{\infty }$$p \rightarrow \infty$时，闵科夫斯基距离即切比雪夫距离(Chebyshev Distance)。

马氏距离

马氏距离，即数据的协方差距离，于欧式距离不同的是它考虑到各属性之间的联系，如考虑性别信息时会带来一条关于身高的信息，因为二者有一定的关联度，而且独立于测量尺度。马氏距离在非奇异变换下是不变的，可用来检测异常值(outliers)。

优点：量纲无关，排除变量之间的相关性干扰。

余弦距离

余弦距离测量两个矢量之间的夹角，而不是两个矢量之间的幅值差。它适用于高维数据聚类时相似度测量。

K-means

优化目标

设数据集有$N$$N$个点，现寻找$k$$k$个中心点$c_1,c_2,...,c_k$$c_1,c_2,...,c_k$，使得：

损失函数：

为了求损失函数的最小值，对损失函数求偏导，并令偏导数为0：

得：

可以看出，新的中心点就是所有该类的质心。

算法步骤

1. 初始化$k$$k$个中心点，$\mathbf{\text{c}}=c_1,c_2,...,c_k$$\textbf{c}=c_1, c_2,...,c_k$

2. 针对数据集中的每个样本点$x_i$$x_i$，计算它到$k$$k$个聚类中心的距离，然后将其分配到距离最近的聚类中心所对应的类别。

3. 针对每个类别$c_j$$c_j$，更新聚类中心

   $$\begin{array}{}\text{(10)}& c_j=\frac{1}{\left|c_j\right|}\sum _{x\in c_j}x\end{array}$$

4. 重复2~3步骤，直到达到某个中止条件（迭代次数、最小误差变化等）。

算法优化

数据预处理

K-means 的本质是基于欧式距离的数据划分算法，均值和方差大的维度将对数据的聚类产生决定性影响。所以未做归一化处理和统一单位的数据是无法直接参与运算和比较的。常见的数据预处理方式有：数据归一化，数据标准化。 ​ 此外，离群点或者噪声数据会对均值产生较大的影响，导致中心偏移，因此我们还需要对数据进行异常点检测。

K值选择

1. 交叉验证

2. 肘方法：loss下降的速度

3. ISODATA

   当属于某个类别的样本数过少时把这个类别去除，当属于某个类别的样本数过多、分散程度较大时把这个类别分为两个子类别。

4. Gap statistic，见 《参考文档-gap.pdf》

   github：milesgranger/gap_statistic: Dynamically get the suggested clusters in the data for unsupervised learning. (github.com)

    

中心点初始化

1. 随机产生：当原始数据符合高斯分布，而随机产生的点如果在同一个组，效果会很差。

2. 最远化：先随机选择一个点，然后选择距离该点最远的点作为第二点，再选择距离前两个点最远的点作为第三点，以此类推。但是，该方法受噪声点影响较大。

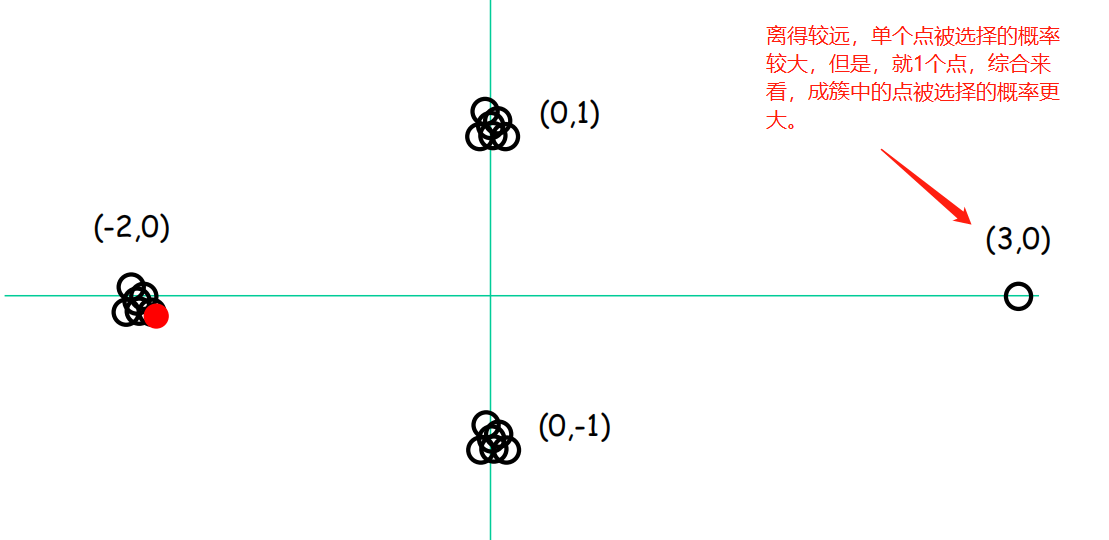
3. k-menas++：对最远化进行了改进，最远化方法直接选择最远的点，k-means++则以一定概率选择每一个点。当然，最远的点概率相对会大，但是如果最远的点仅仅是较少的异常点，而正常的成簇的点虽然距离较近（单个点的概率较小），但点数众多，那么整体上能够选择到该簇中的点作为中心点的概率也会较大（点多力量大）。

   • 随机选择第一个点作为中心点

   • 对第$i=2,3,...,k$$i=2,3,...,k$个中心点

     • 对每个点$j$$j$，计算其到前$i-1$$i-1$个中心点的最短距离，记为$d_j$$d_j$
     • 以正比于$d_j$$d_j$的概率，选择第$j$$j$个点作为中心点

非线性映射

基于欧式距离的 K-means 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布，但这种分布在实际生活中并不常见。面对非凸的数据分布形状时我们可以引入核函数来优化，这时算法又称为核 K-means 算法，是核聚类方法的一种。核聚类方法的主要思想是通过一个非线性映射，将输入空间中的数据点映射到高位的特征空间中，并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率，从而在经典的聚类算法失效的情况下，通过引入核函数可以达到更为准确的聚类结果。

常见问题

为什么会收敛

1. 解释一：每次迭代损失函数都会下降，并且损失函数有下界，因此能够收敛。

2. 解释二：EM算法

   回顾K-means步骤：先随机选择初始节点作为中心点，然后计算每个样本所属类别，再通过类别更新中心点。

   K-Means	EM算法	解释
   确认中心点后，对数据集重新进行标记	E步：求当前参数条件下的Exceptation	找到一个最逼近目标的函数$\gamma$$\gamma$
   根据标记重新求中心点	M步：求似然函数最大化（损失函数最小）时对应的参数	固定函数$\gamma$$\gamma$，更新中心点$c$$c$，即找到当前函数下最优的参数

    

算法复杂度

$\mathbf{\text{O(nkd)}}$$\textbf{O(nkd)}$

适用场景

凸形簇。

如何评估效果

1. 轮廓系数（Silhouette Coefficient）

   • a：内聚度，某点到与其同类的其它点之间的平均距离，反映一个样本点与类内元素的紧密程度。
   • b：分离度，某点到与其最近邻簇中点的平均距离，反映一个样本点与类外元素的紧密程度。

   单个点的轮廓系数为：

   $$\begin{array}{}\text{(11)}& s=\frac{b-a}{max(a,b)}\end{array}$$

   整个数据集的轮廓系数为所有点轮廓系数的均值。

    

   优点：

   • 轮廓系数为-1时表示聚类结果不好，为+1时表示簇内实例之间紧凑，为0时表示有簇重叠。
   • 轮廓系数越大，表示簇内实例之间紧凑，簇间距离大，这正是聚类的标准概念。

   缺点：

   • 对于簇结构为凸的数据轮廓系数值高，而对于簇结构非凸需要使用DBSCAN进行聚类的数据，轮廓系数值低，因此，轮廓系数不应该用来评估不同聚类算法之间的优劣，比如Kmeans聚类结果与DBSCAN聚类结果之间的比较。

    

2. CH index

优缺点比较

优点：

• 容易理解，聚类效果不错，虽然是局部最优， 但往往局部最优就够了；
• 处理大数据集的时候，该算法可以保证较好的伸缩性；
• 当簇近似高斯分布的时候，效果非常不错；
• 算法复杂度低。

缺点：

• K 值需要人为设定，不同 K 值得到的结果不一样；
• 对初始的簇中心敏感，不同选取方式会得到不同结果；
• 对异常值敏感；
• 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。

层次聚类

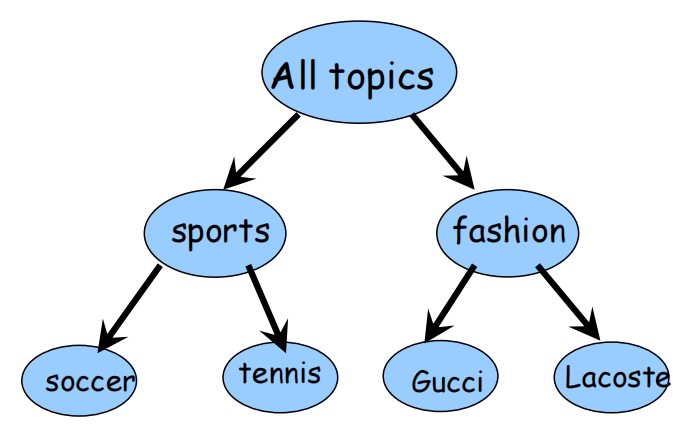
算法原理

Top-down(divisive)

1. 将数据分为2组(e.g. 2-means)

2. 递归地处理每一组

   

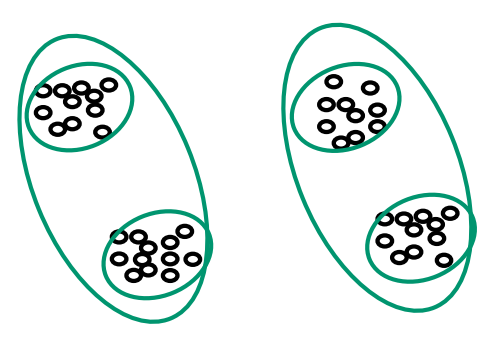
Bottom-up(agglomerative)

1. 每两个点形成一个cluster

2. 重复合并两个最近的cluster。

   如何度量两个cluster之间的距离？可以使用两个cluster两两点之间min/max/avg距离作为两个cluster之间的距离。

常见问题

时间复杂度

$\text{Error: '^' allowed only in math mode}$$\textbf{O(n^3)}$

DBSCAN

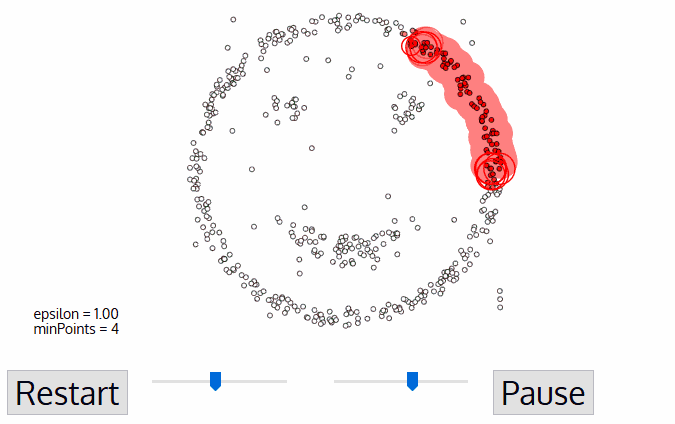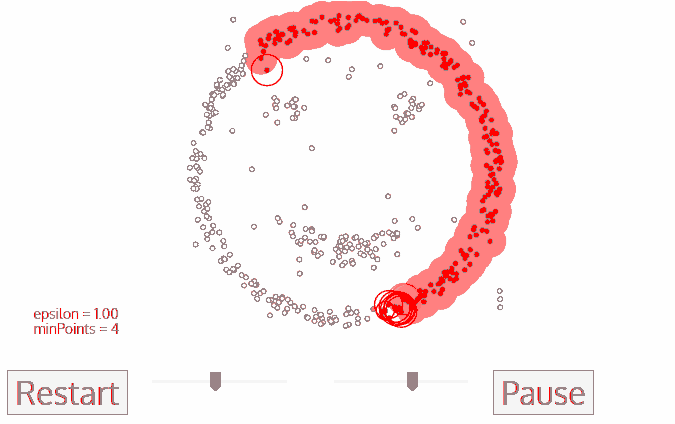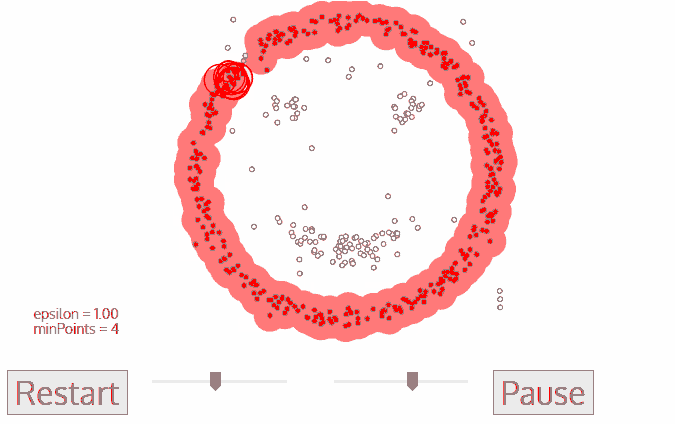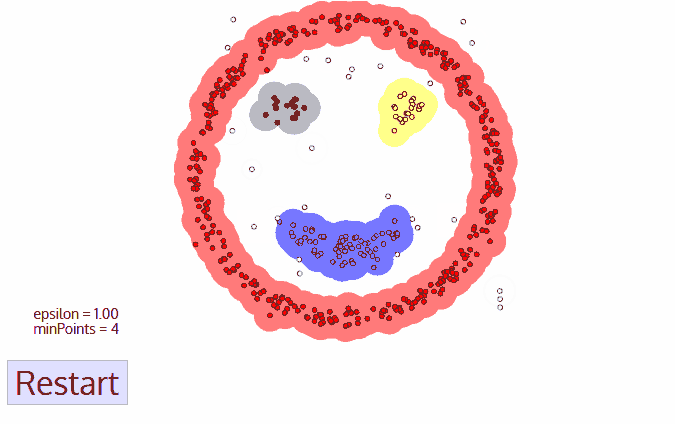
基于密度的聚类算法。DBSCAN的核心思想是从某个核心点出发，不断向密度可达的区域扩张，从而得到一个包含核心点和边界点的最大化区域，区域中任意两点密度相连。

优点：

1. 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。
2. 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。
3. 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

缺点：

1. 如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。
2. 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
3. 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值$ϵ$$\epsilon$，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。

GMM

如何选择聚类中心数？AIC、BIC

谱聚类

待补充。

参考链接

1. 2.3. Clustering — scikit-learn 0.24.2 documentation

2. DBSCAN密度聚类算法 - 刘建平Pinard - 博客园 (cnblogs.com)

3. 谱聚类（spectral clustering）原理总结 - 刘建平Pinard - 博客园 (cnblogs.com)