分类
混淆矩阵

准确率
准确率:预测正确的结果占总样本的百分比。
问题:样本不均衡时,该指标不能很好得衡量结果。例如,正样本占比95%,负样本占比为5%,如果将所有样本预测为正样本,则准确率为95%。
精确率
精确率:在所有被预测为正的样本中实际为正样本的概率。
召回率
召回率:又叫查全率,在实际为正的样本中被预测为正样本的概率。
使用场景:以网贷违约为例,相对正常用户,更关心违约用户,不能放过任何一个违约用户。
召回率越高,“坏用户”被预测出来的概率越高,宁可错杀一千,绝不放过一个。
F1-Score
适用场景:对precision和recall要求都较高的情况下,可以选择F1-score。
micro-F1
计算方法:计算所有类别总的Precision和Recall,然后再计算F1
效果特点:当样本不均衡时,更容易受到常见类别的影响
适用场景:注重样本真实分布,只考虑全局结果
macro-F1
计算方法:单独计算每个类别的F1值,然后取各类F1的均值作为最终F1
效果特点:相对更考虑稀有类别的影响,同时受高P&R的类别的影响较大
适用场景:样本不均衡,且各个类别同等重要,可保障小样本的性能
ROC and PR
ROC
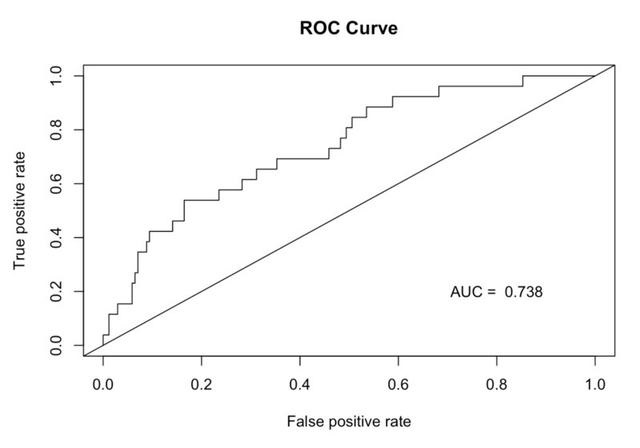
当一个样本被分类器判为正例,若其本身为正例,则
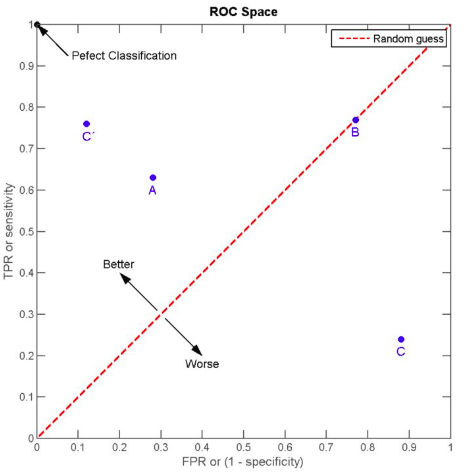
- 从所有正例随机选取一个样本
- 物理意义:给定正样本
- 对样本不均衡不敏感。换言之,
假设正样本对数为
对预测概率,枚举阈值,分别计算
假设正样本排在负样本之前的正负样本对数为
类似方法2,另一种方式计算
PR
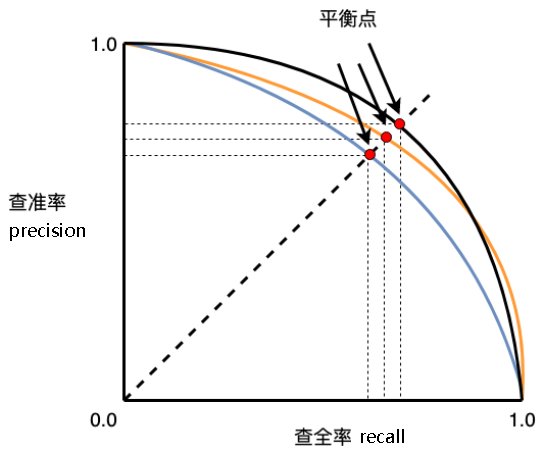
ROC vc PR
- ROC曲线由于兼顾正例与负例,所以适用于评估分类器的整体性能,相比而言PR曲线完全聚焦于正例。
- 如果有多份数据且存在不同的类别分布,比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同,这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响,则ROC曲线比较适合,因为类别分布改变可能使得PR曲线发生变化时好时坏,这种时候难以进行模型比较;反之,如果想测试不同类别分布下对分类器的性能的影响,则PR曲线比较适合。
- 如果想要评估在相同的类别分布下正例的预测情况,则宜选PR曲线。
- 类别不平衡问题中,ROC曲线通常会给出一个乐观的效果估计,所以大部分时候还是PR曲线更好。
- 样本类别分布大致均衡,可以使用
- 样本分布非常不均衡,可以使用
回归
MAE
受异常值干扰较明显。
MSE
RMSE
MAPE
参考链接
- ROC-AUC 与 PR-AUC 的区别与联系 - 知乎 (zhihu.com)
- 精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么? - 知乎 (zhihu.com)
- The Probabilistic Interpretation of AUC (madrury.github.io)
- AUC计算方法与Python实现代码 - 云+社区 - 腾讯云 (tencent.com)