EM算法
背景知识
相似三角形
- 定理:两角分别对应相等的两个三角形相似。
- 定理:相似三角形任意对应线段的比等于相似比。
梯形中位线推论
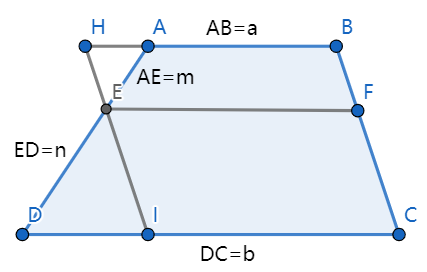
已知:在梯形中,为边上的任意一点,,且与相交与点。
结论:
证明:过做直线平行于,由相似三角形定理可知,。
所以,
化简可得:
特别地,当时,
Jensen(琴生)不等式
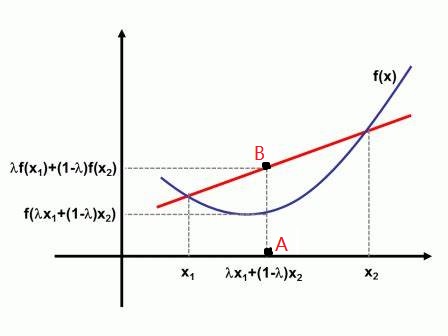
若是凸函数,则:
证明1:令,直线与曲线相交的两点分别为,。
根据直线两点式,可得直线方程为
当时,
证明2:令
因为,所以。
因为
根据梯形推导公式可得:
将上式中的推广到个同样成立,即:
其中,
如果将看做概率分布,则在概率论中:
其中,是凸函数,是随机变量,为的期望
期望
对随机变量,对应的概率为,则随机变量的期望为:
三硬币模型引入
问题:假设有3枚硬币,分别记作A,B,C。这些硬币正面出现的概率分别是 和。进行如下掷硬币试验: 先掷硬币A,根据其结果选出硬币B或硬币C,正面选硬币B,反面选硬币C;然后掷选出的硬币,掷硬币的结果,出现正面记作1,出现反面记作0;独立地重复n次试验(这里,n=10),观测结果如下:
,,,,,,,,,
假设只能观测到掷硬币的结果,不能观测掷硬币的过程。问如何估计三硬币正面出现的概率,即三硬币模型的参数。
解:对每一次试验可如下建模
其中,随机变量是观测变量,表示一次试验的结果是或;随机变量是隐变量,表示未观测到的掷硬币的结果;是模型参数。将观测数据表示为,未观测到的数据表示为。 则观测数据的似然函数为:
考虑求模型参数的极大似然估计,即使用对数似然函数来进行参数估计,可得:
上式没有解析解,也就是没有办法直接通过求导方式解出的值,只能使用迭代法进行求解。
EM算法
为什么需要EM算法
概率模型有时候既含有观测变量又含有隐变量。如果概率模型的变量都是观测变量,那么给定数据,可以直接使用极大似然法估计或贝叶斯估计进行求解。但是,当模型含有隐变量时,就不能简单地使用这些估计方法。
EM算法就是解决含有隐变量的概率模型参数的极大似然估计。
EM算法推导
当面对含有隐变量的模型时,目标是极大化观测数据关于参数的对数似然函数,即极大化:
注意到这一极大化的主要困难是上式中有未观测数据并有包含和(为离散型时)或 者积分(为连续型时)的对数。EM算法采用的是通过迭代逐步近似极大化 。
假设在第次迭代后 的估计值是 , 我们希望新的估计值 能使 增加,即 并逐步达到极大值。为此,我们考虑两者的差:
将移项,令:
则:
即函数是的一个下界函数。
此时,若设使得达到极大,也就意味着:
由于:
进一步可推得:
即:
因此,任何能使得增大的,也可以使增大。于是,问题就转化为求解能使得到达极大的,即:
至此,完成了EM算法的一次迭代,求出的作为下一次迭代的初始。
综上所述,可以总结出EM算法的“E步”和“M步”分别为:
步:导出函数
计算完全数据的对数似然函数关于给定观测数据和当前参数下对未观测数据的条件概率分布的期望,也即函数:
步:函数极大
求使得函数达到极大的。
使用EM求解三硬币模型
求解思路:
- 步:导出函数
- 步:求使得函数达到极大的
E步:导出Q函数
单独考察
所以,
将其带回函数可得:
由于:
所以,函数的最终形式为:
求Q函数达到极大的参数
该步骤求使得函数达到极大的。
对求偏导
对函数关于求一阶偏导数,并令一阶偏导数为0:
令上式为0,可得:
对求偏导
对函数关于求一阶偏导数,并令一阶偏导数为0:
令上式等于0可得:
对求偏导
对函数关于求一阶偏导数,并令一阶偏导数为0:
令上式等于0可得:
总结
综上所述,为了求函数的极大值,可使用如下公式进行参数迭代:
参考文档
从最大似然到EM算法:一致的理解方式 - 科学空间|Scientific Spaces
(47条消息) EM算法之三硬币模型求解zsdust的博客-CSDN博客三硬币模型
人人都懂EM算法 - 知乎 (zhihu.com)
EM算法详解 - 知乎 (zhihu.com)
【机器学习】EM——期望最大(非常详细) - 知乎 (zhihu.com)

