PCA2021-10-06
背景知识
协方差
为两个一维随机变量,它们的协方差为:
协方差矩阵
对多维随机变量:
其中,,为列向量
计算其两两维度之间的协方差,各协方差组成了一个的矩阵,称为协方差矩阵,记为。矩阵内的元素:
样本协方差矩阵:
若的列均值为0,则:
PCA原理
降维概述
不加思索地认为,对矩阵通过线性变换降维后,数据越分散,效果越好。如何度量数据的分散程度?各维度的方差越大,数据越分散。概括一下,降维后,各维度方差越大,降维效果越好。
举例:将二维数据降到一维,如果集中到了一点,那么数据就不具备可分性,自然可以认为降维效果不好。说明降维后数据越分散、越具有可分性,降维效果越好。在PCA中,选择“方差”作为衡量数据分散性的指标。
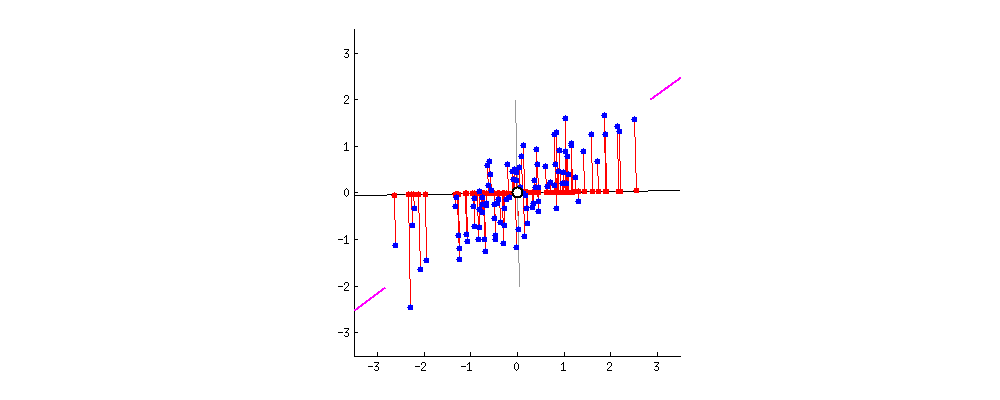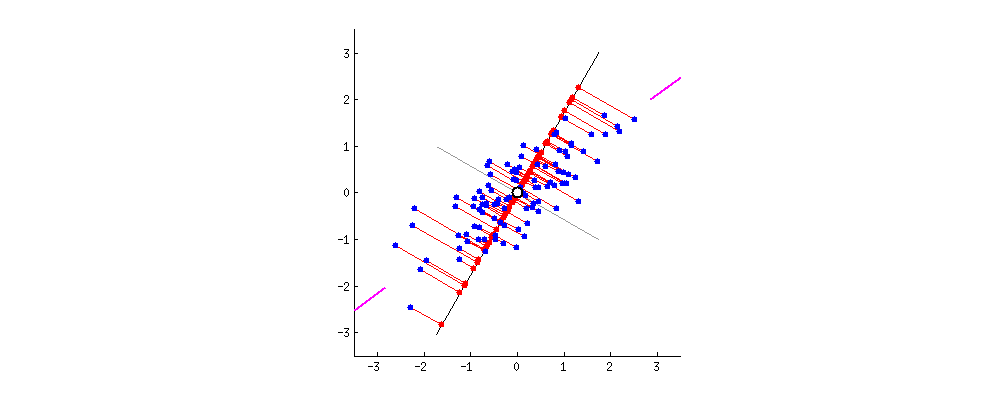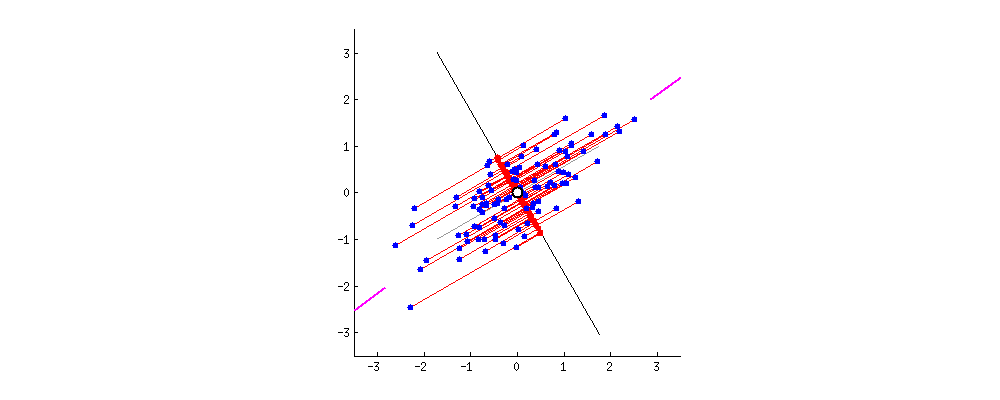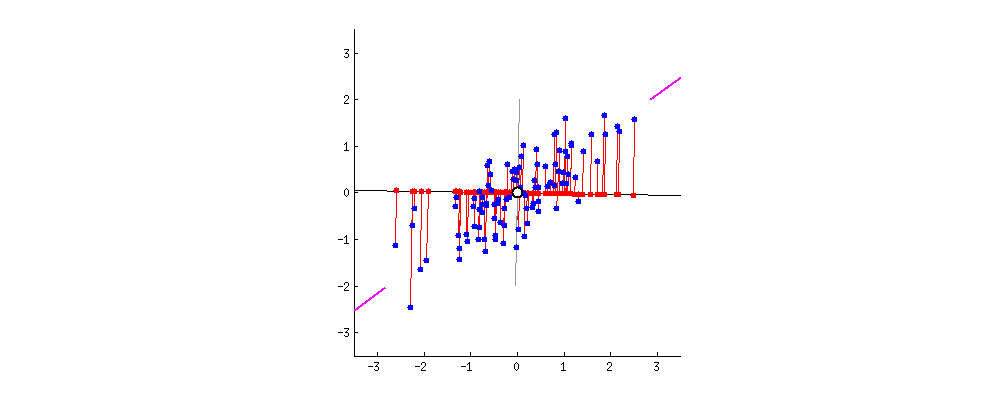
降维概述:给定原始矩阵及线性变换矩阵,通过线性变换,将矩阵由维降到维,得到矩阵,降维后的维度,又称为主成分个数。
原理推导
假设:
- 已经对矩阵做了标准化,其均值。
- 矩阵为正交矩阵。
首先,考虑求第一主成分:
其中, 求的方差:
其中,为矩阵的协方差矩阵 优化目标:
定义拉格朗日函数:
求函数对的导数并令导数为0:
求得:
所以,为协方差矩阵的特征值,为对应的单位特征向量。
进一步,优化目标可化简为:
假设是的第一大特征值对应的单位特征向量,显然,和是以上问题的最优解。
然后,考虑求第二主成分:
注意到:
说明,等式约束是等价的。
定义拉格朗日函数:
求函数对的导数并令导数为0:
将上式左乘以得:
此式前两项为0,且,所以,。根据式可得:
所以,是协方差矩阵的特征值,为对应的单位特征向量。于是,目标函数:
假设是的第二大特征值对应的单位特征向量,显然,和是以上问题的最优解。
一般地,的第主成分是,并且,这里为第大的特征值并且为对应的单位特征向量。
综上所述,为将进行降维,只需要求其协方差矩阵的特征向量即可。
PCA求解
协方差矩阵的特征值分解法
数据规范化处理
将做规范化处理,处理后,每一列的均值为0。
每列均值每列标准差 计算协方差矩阵
求协方差矩阵的特征值和特征向量
特征值(从大到小排列):
特征向量:
求个主成分
计算k个主成分的方差贡献率
数据矩阵的奇异值分解算法
给定矩阵,并且该矩阵每列均值为0。构造一个新矩阵:
那么:
不难得知,为的协方差矩阵。
根据SVD分解定理:
所以,为协方差矩阵的特征向量,同时也是的右奇异矩阵。
至此,将求解矩阵协方差矩阵的特征向量,转为求解矩阵的右奇异矩阵。
基于SVD分解的PCA降维求解过程:
构造新矩阵
对矩阵进行截断奇异值分解
其中,是矩阵,是阶对角矩阵,是矩阵 矩阵是个样本主成分的线性变换矩阵。
降维:维 维
示例
问题:给定矩阵,从2维降到1维。
降维步骤:
数据标准化处理:减均值,除以标准差
求协方差矩阵
求协方差矩阵的特征值和特征向量
特征值:
特征向量:
求降维后的数据(第一主成分)
求第一主成分的方差贡献
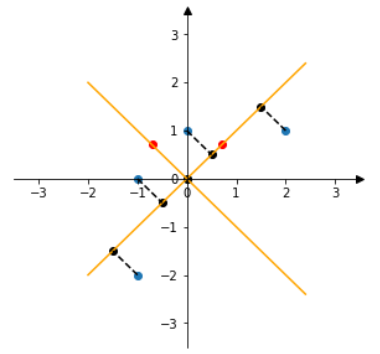
降维结果可视化:
参考链接
- PCA与SVD应用中负号问题 - 深海里的猫 - 博客园 (cnblogs.com)
- 主成分分析(Principle Component Analysis) - swolf的博客 (mrswolf.github.io)
- 使用numpy来理解PCA和SVD - 知乎 (zhihu.com)
- CodingLabs - PCA的数学原理

