PageRank2022-05-21
简介
PageRank算法的基本思想是在有向图上定义一个随机游走模型,即一阶马尔可夫链,描述随机游走者沿着有向图随机访问各个结点的行为。在一定条件下,极限情况访问每个结点的概率收敛到平稳分布,此时,各个结点的平稳概率值就是其PageRank值,表示结点的重要度。
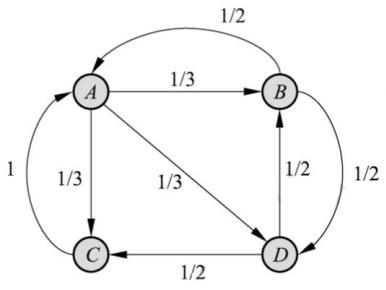
上图是一个有向图,假设是简化的互联网图例,结点A、B、C、D表示网页,结点之间的有向边表示网页之间的超链接,边上的权值表示网页之间随机跳转的概率。
假设有一个浏览者,在网页上随机游走。如果浏览者在网页A,则下一步有的概率转移到网页B、C、D。其余类似。
直观上,对一个网页:
- 如果指向该网页的超链接越多,随机跳转到该网页的概率也就越高,那么该网页的PageRank值越高。
- 如果指向该网页的PageRank值越高,随机跳转到该网页的概率也就越高,那么该网页的PageRank值越高。
PageRank的计算可以在互联网的有向图上进行,通常是一个迭代过程。先假设一个初始分布,通过迭代,不断计算所有网页的PageRank值,直到收敛为止。
随机游走模型
给定一个含有n个结点的的有向图,在有向图上定义随机游走(Random walk)模型,即一阶马尔可夫链,其中结点表示状态,有向边表示状态之间的转移,假设从一个结点到其可直接到达的所有结点的转移概率相等。具体地,转移矩阵是一个阶矩阵:
第行第列的元素取值规则如下:如果结点有个有向边连出,并且结点是其连出的一个结点,则,否则, 。
对上图,可得到状态转移矩阵:

转移矩阵具有如下性质:
即每个元素非负,每列元素之和为1,矩阵为随机矩阵。
随机游走在某个时刻t访问各个结点的概率分布就是马尔可夫链在时刻t的状态分布,可以用一个n维列向量表示,那么,在时刻t+1访问各个结点的概率分布满足:
给定一个包含n个结点的强连通且非周期性的有向图,在其基础上定义随机游走模型,假设转移矩阵,在时刻访问各个结点的概率分布为:
则以下极限存在:
极限向量表示马尔可夫链的平稳分布,满足:
给定一个包含n个结点的强连通且非周期性的有向图,在有向图上定义随机游走模型,即一阶马尔可夫链。随机游走的特点是从一个结点经有向边到其所连接结点的转移概率相等,转移矩阵为。这个马尔可夫链具有平稳分布:
平稳分布称为这个有向图的PageRank。的各个分量称为各个结点的PageRank值。
根据PageRank定义,显然有:
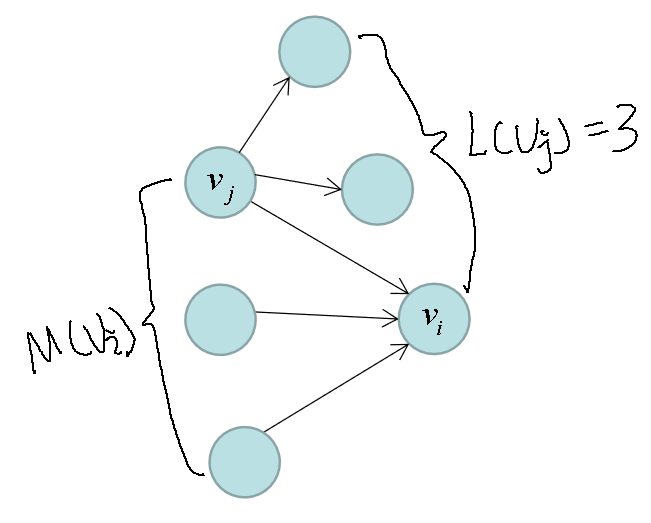
表示指向结点的集合表示结点连出的有向边的个数 PageRank公式解释如下:
一般的马尔可夫链未必具有平稳性,为了解决该问题,PageRank一般定义的想法是在基本定义的基础上导入平滑项。
考虑另外一个完全随机游走的模型,其转移矩阵的元素全部为,即从任意一个结点转移到任意一个结点的概率都是。两个转移矩阵的线性组合又构成了一个新的转移矩阵,在其上可以定义一个新的马尔可夫链。
容易证明,组合后的马尔可夫链一定具有平稳性,且平稳分布满足:
是系数,称为阻尼因子是维向量,表示的是有向图的是所有分量为的维向量 上式中,第一项表示依照转移概率矩阵访问各个结点的概率,第二项表示完全随机访问各个结点的概率。
阻尼因子值由经验决定,一般取。当接近1时,随机游走模型主要依照转移矩阵进行,当接近0时,随机游走主要以等概率随机访问各个结点。
依照上式,可以写出每个结点的PageRank,以下是PageRank的一般定义:
第二项为平滑项,由于采取平滑项,所有结点的PageRank值都不会为0,具有以下性质:
的一般定义: 给定一个含有n个结点的任意有向图,在有向图上定义一个一般的随机游走模型,即一阶马尔可夫链。一般的随机游走模型的转移矩阵由两部分线性组合组成,一部分是有向图的基本转移矩阵,表示从一个结点到其连出的所有结点的转移概率相等,另一部分是完全随机的转移矩阵,表示从任意一个结点到任意一个结点的转移概率都是,线性组合系数为阻尼因子。这个一般随机游走的马尔可夫链存在平稳分布,记作。定义平稳分布向量为这个有向图的一般PageRank。由公式下述公式决定:
其中是所有分量为的维向量 一般PageRank的定义意味着互联网浏览者在任意一个网页时,按照以下方式在网上随机游走:
- 以概率决定按照超链接随机跳转,即从当前网页以等概率跳转到与其直接相连的网页。
- 以概率决定完全随机跳转,此时以等概率跳转到任意一个网页。
第二个机制保证即使某个网页没有连接出去的超链接,也可以跳出该网页。该机制使得PageRank适用于任何结构的网络。
迭代计算
根据迭代公式计算即可,具体如下述算法所示。
算法的迭代算法
输入: 含有 个结点的有向图, 转移矩阵 , 阻尼因子 , 初始向量 ;
输出: 有向图的 PageRank 向量 。
(1) 令
(2) 计算
(3) 如果 与 充分接近, 令 , 停止迭代。
(4) 否则, 令 , 执行步 (2)。
幂法
针对一般的PageRank,转移矩阵可写作:
其中,是阻尼因子是所有元素为的阶方阵 根据Perron-Frobenius定理,一般PageRank的向量是矩阵的主特征向量,主特征值是1。
所以,可以使用幂法近似计算一般PageRank。
算法幂法求
输入: 含有 个结点的有向图, 有向图的转移矩阵 , 系数 , 初始向量 , 计算精度 ;
输出: 有向图的 PageRank,即向量 。
(1) 令 , 选择初始向量
(2) 计算有向图的一般转移矩阵
(3) 迭代并规范化结果向量
注意:此处使用无穷范数,即 (4) 当 时, 令 , 停止迭代。
(5) 否则, 令 , 执行步 (3)。
(6) 对 进行规范化处理, 使其表示概率分布。
代数算法
按照一般PageRank的定义式:
于是,对上式进行变形:
其中,是单位矩阵 当时,线性方程组的解存在且唯一。
这样,可以通过求逆矩阵得到有向图的一般PageRank。


