SVM另一种思考2021-09-25
目标函数推导
两种距离
同比例缩放仅影响函数间隔,不会影响几何间隔。
等比例缩放示例:
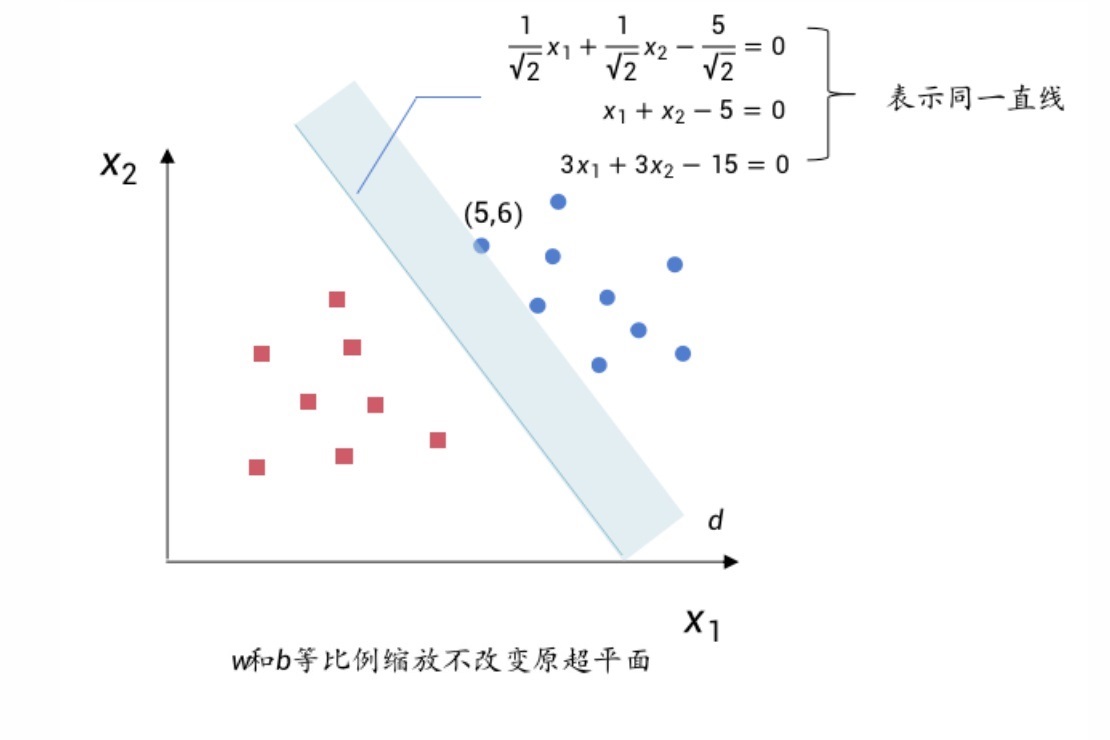
定义优化目标
优化目标的含义:对不同的,比较最小几何距离,然后选择使得最小几何距离最大的作为目标解。
如何对优化目标进行简化?对于给定的, 为任意的正数,同时也对应一个确定的超平面。但是,因为同比例缩放超平面的参数(w,b)并不改变超平面的位置,即同比例缩放后仍是同一超平面,因此,给定一个超平面,可以有无数个与之对应。这就意味着,公式()优化目标的解不唯一,需要增加约束条件,以限定唯一的超平面。
比如,限定,但该约束不能简化公式()。
实际中采用的约束是限制最小的函数距离为1,即距离超平面最近最近的那个点,其函数距离为1。在该条件下,也能唯一被确定。
加入约束条件后的求解目标:
几何距离推导
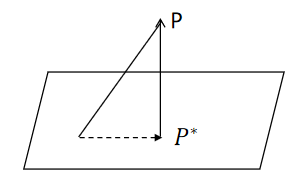
平面方程为,点为平面上一点,点为平面为一点,向量垂直于平面。
两边同时乘以得:
参考文档
- SVM最大间隔超平面学习笔记及对函数间隔设置为1的思考 - 知乎 (zhihu.com)



