SVM心路历程2022-01-25

SVM原理推导定义任务决策函数标准化计算街宽定义优化目标定义拉格朗日函数核方法神经网络对偶问题转化SMO算法附录二范数求导

SVM原理推导

定义任务

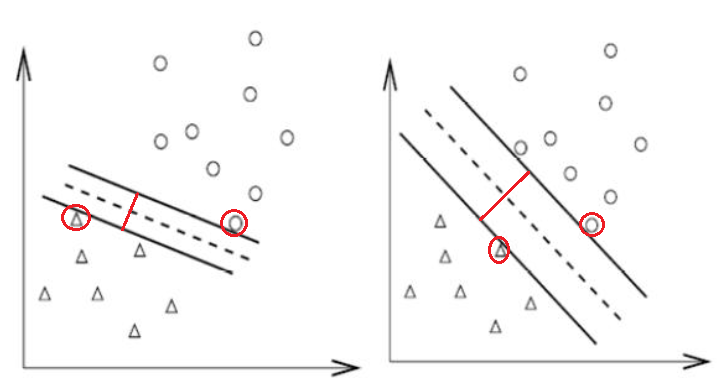
任务：对线性可分的二分类问题，寻找一条直线，对于距离该直线最近的正负样本点，使得它们到直线的距离相等，且它们之间的距离最大。即寻找最宽的路，将正负样本分开。

如下图所示，右侧的决策边界要优于左侧决策边界。

决策边界对比2

$\overrightarrow{w}$ $C$ 为原点到决策边界的距离，则决策函数为：

\begin{matrix} (1) & \begin{matrix} {\begin{matrix} \vec{w} \cdot \vec{x} > C, t h e n + \\ \vec{w} \cdot \vec{x} < C, t h e n - \end{matrix} \end{matrix} \end{matrix}

稍作化简，可得：

\begin{matrix} (2) & \begin{matrix} {\begin{matrix} \vec{w} \cdot \vec{x} + b > 0, t h e n + \\ \vec{w} \cdot \vec{x} + b < 0, t h e n - \end{matrix} \end{matrix} \end{matrix}

$y$ 做如下定义：

\begin{matrix} (3) & \begin{matrix} y = {\begin{matrix} 1, + \\ - 1, - \end{matrix} \end{matrix} \end{matrix}

则决策函数应该满足：

\begin{matrix} (4) & y (\vec{w} \cdot \vec{x} + b) > 0 \end{matrix}

决策函数标准化

对决策函数加入距离限制，比如要求最近的点到决策边界的函数间隔至少为1，则决策函数：

\begin{matrix} (5) & \begin{matrix} y (\vec{w} \cdot \vec{x} + b) ⩾ 1 \\ x \in 训 练 集 \end{matrix} \end{matrix}

含义：正负样本点距离决策边界的最近距离为1。对于等于1的点，我们称之为支持向量。

计算街宽

\begin{matrix} (6) & \begin{aligned} W I D T H & = (\vec{x_{+}} - \vec{x_{-}}) \cdot \frac{\vec{w}}{| \vec{w} |} \\ = \frac{2}{| \vec{w} |} \\ \vec{x_{+}} 和 \vec{x_{-}} 均 为 支 持 向 量 \end{aligned} \end{matrix}

定义优化目标

\begin{matrix} (7) & \begin{matrix} m a x \frac{2}{| \vec{w} |} \\ \Rightarrow m i n | \vec{w} | \\ \Rightarrow {\begin{matrix} m i n \frac{1}{2} {‖ \begin{matrix} \vec{w} \end{matrix} ‖}_{2}^{2} \\ s . t . y_{i} (\vec{w} \cdot \vec{x_{i}} + b) ⩾ 1, i = 1. . . N \end{matrix} \end{matrix} \end{matrix}

定义拉格朗日函数

\begin{matrix} (8) & \begin{matrix} L (α, w, b) = \frac{1}{2} {‖ \begin{matrix} \vec{w} \end{matrix} ‖}_{2}^{2} + \sum_{i = 1}^{N} α_{i} [1 - y_{i} (\vec{w} \cdot \vec{x_{i}} + b)] \\ \vec{α} = (α_{1}, α_{2}, \dots, α_{N}) \geq 0 \end{matrix} \end{matrix}

$L$ 最小 $L$ $\overrightarrow{w}$ $b$ 求导：

\begin{matrix} (9) & \begin{matrix} \frac{\partial L}{\partial \vec{w}} = \vec{w} - \sum_{i = 1}^{N} α_{i} y_{i} x_{i} = 0 \\ \frac{\partial L}{\partial b} = - \sum_{i = 1}^{N} α_{i} y_{i} = 0 \end{matrix} \end{matrix}

$\overrightarrow{w}$ 的最优解：

\begin{matrix} (10) & \begin{matrix} \vec{w^{*}} = \sum_{i = 1}^{N} α_{i} y_{i} x_{i} \\ \sum_{i = 1}^{N} α_{i} y_{i} = 0 \end{matrix} \end{matrix}

$b$ $y_i(\overrightarrow{w} \cdot \overrightarrow{x_i} + b) = 1$ 进行求解。

至此，求得决策边界：

\begin{matrix} (11) & \begin{matrix} {\begin{matrix} \sum_{i = 1}^{N} α_{i} y_{i} (\vec{x_{i}} \cdot \vec{x_{n e w}}) + b > 0, t h e n + \\ \sum_{i = 1}^{N} α_{i} y_{i} (\vec{x_{i}} \cdot \vec{x_{n e w}}) + b < 0, t h e n - \end{matrix} \end{matrix} \end{matrix}

核方法

\begin{matrix} (12) & \begin{matrix} L = \sum_{i = 1}^{N} α_{i} - \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}), x \in 训 练 集 \\ 注 ： 由 此 可 见 ， L 取 决 于 训 练 集 x_{i} \cdot x_{j} \end{matrix} \end{matrix}

定义：

\begin{matrix} (13) & K (x_{i}, x_{j}) = Φ (x_{i}) \cdot Φ (x_{j}) \end{matrix}

$K(x_i,x_j)$ $\Phi$ 为变换函数。左侧为点乘后的变换，右侧为变换后的点乘，核方法本质是将变换后的点乘改为点乘后的变换。我们不需要知道如何变换，只需要知道变换后的结果。

神经网络

从神经网络的角度理解，SVM的本质是通过全连接变换，采用hinge-loss作为损失函数的分类问题。

SVM神经网络

hinge-loss（经验风险）为：

\begin{matrix} (14) & \begin{matrix} L (y \cdot (w \cdot x + b)) = [1 - y \cdot (w \cdot x + b)]_{+} \\ 其 中 ， [z]_{+} {\begin{matrix} z, z > 0 \\ 0, z <= 0 \end{matrix} \end{matrix} \end{matrix}

为了防止过拟合，实际优化目标还会加入正则化项（结构风险）：

\begin{matrix} (15) & \begin{matrix} m i n {[1 - y \cdot (w \cdot x + b)]_{+} + λ | | w | |^{2}}_{w, b} \\ 其 中 ， [z]_{+} {\begin{matrix} z, z > 0 \\ 0, z <= 0 \end{matrix} \end{matrix} \end{matrix}

实现代码为：


x
1
class LinearSVM(nn.Module):
2
    def __init__(self):
3
        super(LinearSVM, self).__init__()
4
        self.linear = nn.Linear(in_features=2, out_features=1)
5
    def forward(self, x):
6
        y = self.linear(x)
7
        return y
8
    
9
svm = LinearSVM()
10
optimizer = optim.SGD(svm.parameters(), lr=0.1)
11

12
batch_size = 1
13
epoch_num = 30
14
N = 500
15

16
for epoch in range(1,epoch_num+1):
17
    for i in range(0, N, batch_size):
18
        x = torch.Tensor(X[i: i+batch_size])
19
        y = torch.Tensor(Y[i: i+batch_size])
20
        
21
        y_pred = svm(x)
22

23
        loss = torch.mean(torch.clamp(1 - y_pred * y, min=0))       # hinge loss
24
        loss += 0.01 * torch.mean(svm.linear.weight ** 2) / 2       # l2 pently
25

26
        loss.backward()
27
        optimizer.step()
28
        optimizer.zero_grad()
29

对偶问题转化

$1. 原始问题：$

\begin{matrix} (16) & \begin{matrix} L (α, w, b) = \frac{1}{2} {‖ \begin{matrix} \vec{w} \end{matrix} ‖}_{2}^{2} + \sum_{i = 1}^{N} α_{i} [1 - y_{i} (\vec{w} \cdot \vec{x_{i}} + b)] \\ \vec{α} = (α_{1}, α_{2}, \dots, α_{N}) \geq 0 \end{matrix} \end{matrix}

$2. 对偶函数：$

\begin{matrix} (17) & g (α) = min_{w, b} L (α, w, b) \end{matrix}

$3. 对偶问题：$

\begin{matrix} (18) & max_{α, α \geq 0} g (α) = max_{α, α \geq 0} min_{w, b} L (α, w, b) \end{matrix}

$4. 求解对偶函数：$

\begin{matrix} (19) & \begin{aligned} \nabla_{w} L (w, b, α) = w - \sum_{i = 1}^{N} α_{i} y_{i} x_{i} = 0 \\ \nabla_{b} L (w, b, α) = - \sum_{i = 1}^{N} α_{i} y_{i} = 0 \end{aligned} \end{matrix}

$解得：$

\begin{matrix} (20) & \begin{aligned} w = \sum_{i = 1}^{N} α_{i} y_{i} x_{i} \\ \sum_{i = 1}^{N} α_{i} y_{i} = 0 \end{aligned} \end{matrix}

$对L(\alpha,w,b)化简得：$

\begin{matrix} (21) & \begin{aligned} L (w, b, α) & = \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) - \sum_{i = 1}^{N} α_{i} y_{i} ((\sum_{j = 1}^{N} α_{j} y_{j} x_{j}) \cdot x_{i} + b) + \sum_{i = 1}^{N} α_{i} \\ = - \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) + \sum_{i = 1}^{N} α_{i} \end{aligned} \end{matrix}

$所以，对偶函数为：$

\begin{matrix} (22) & g (α) = min_{w, b} L (α, w, b) = - \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) + \sum_{i = 1}^{N} α_{i} \end{matrix}

$5. 对偶函数极大化，即将原问题转化为对偶问题：$

\begin{matrix} (23) & \begin{array}{ll} max_{α} & - \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) + \sum_{i = 1}^{N} α_{i} \\ s.t. & \sum_{i = 1}^{N} α_{i} y_{i} = 0 \\ α_{i} ⩾ 0, i = 1, 2, \dots, N \end{array} \end{matrix}

$将问题改为等价的 \min 问题：$

\begin{matrix} (24) & \begin{array}{ll} min_{α} & \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) - \sum_{i = 1}^{N} α_{i} \\ s.t. & \sum_{i = 1}^{N} α_{i} y_{i} = 0 \\ α_{i} ⩾ 0, i = 1, 2, \dots, N \end{array} \end{matrix}

SMO算法

待补充。

附录

二范数求导

\begin{matrix} (25) & {‖ \begin{matrix} \vec{w} \end{matrix} ‖}_{2}^{2} = {\vec{w}}^{T} \cdot \vec{w} = w_{1}^{2} + w_{2}^{2} + . . . + w_{n}^{2} \end{matrix}

\begin{matrix} (26) & \frac{\partial {\vec{w}}^{T} \cdot \vec{w}}{\partial \vec{w}} = 2 \vec{w} \end{matrix}

$w_1^2 + w_2^2 + ... + w_n^2$ $\overrightarrow{w}$ 中的每个变量求偏导。