单层前馈神经网络2022-01-02
单层前馈神经网络
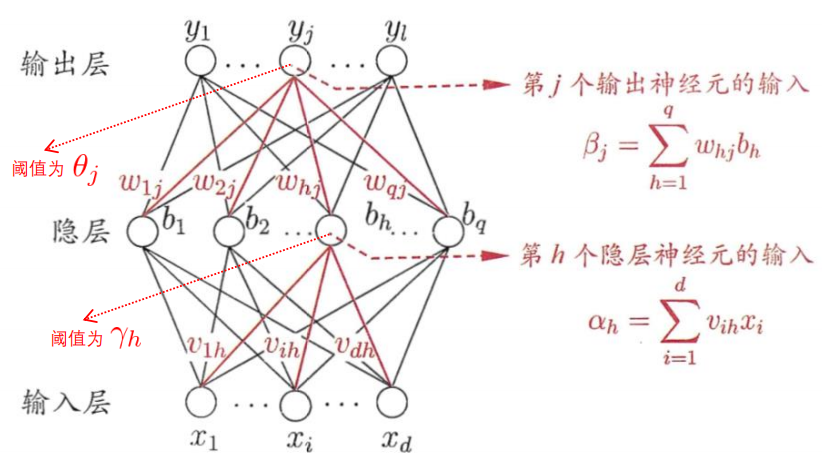
符号解释
- :输入的第个数据,共维
- :输入层到隐藏层的权重,为隐藏层结点的个数
- :输入层到隐藏层的阈值(偏置)
- :隐藏层的输入
- :隐藏层的输出
- :隐藏层到输出层的权重,为输出层结点的个数
- :隐藏层到输出层的阈值(偏置)
- ,输出层的输入
- :输出层的输出
- :输出层的label
- :sigmoid函数,其导数特点为
- :损失函数
前馈计算
输入层到隐藏层
隐藏层到输出层
其中, 损失函数
反向传播
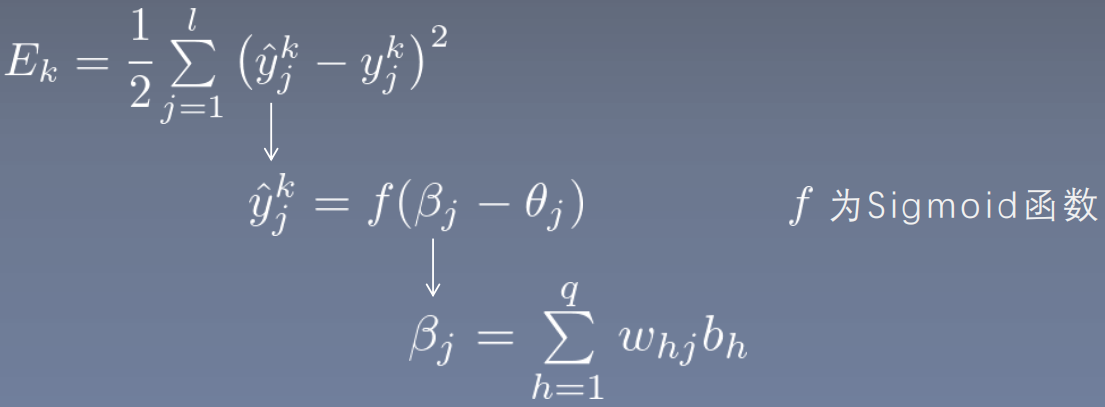
因此,
分开计算:
令:
所以:
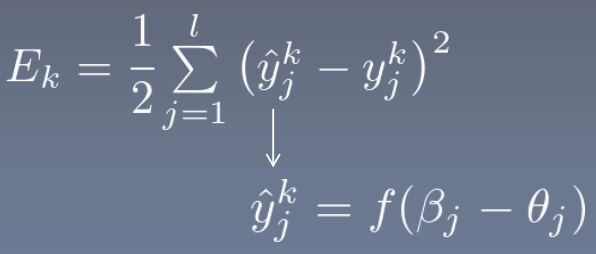
因此,
所以:
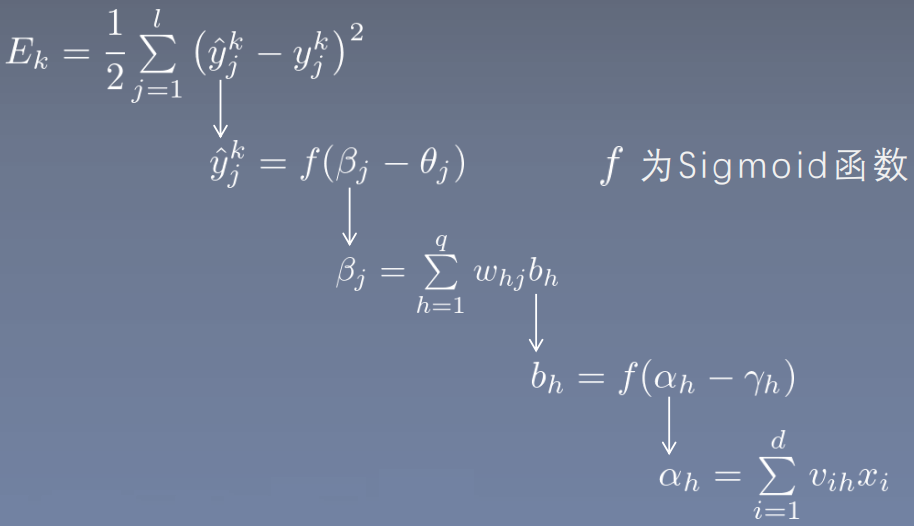
因此,
分开计算,
令:
所以,
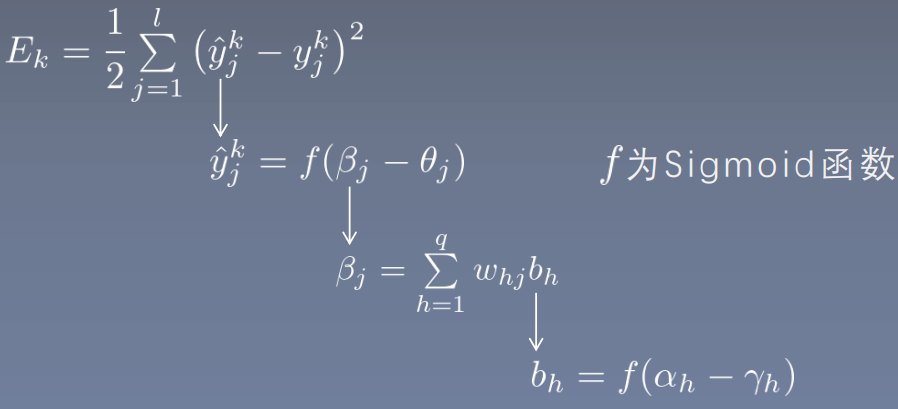
因此,
所以: