LSA简介

LSA（latent semantic analysis），即潜在语义分析，是一种无监督方法。主要用于文本的话题分析，其特点是通过矩阵分解发现文本与单词之间的基于话题的语义关系。具体地，将文本集合表示为单词-文本矩阵，对单词-文本矩阵进行分解，从而得到话题向量空间，即文本在话题向量空间的表示。

矩阵分解可以选择奇异值分解（SVD）或非负矩阵分解。

单词向量空间

给定一个含有$n$$n$个文本的集合$D=\{d_1,d_2,\cdots ,d_n\}$$D=\{d_1, d_2, \cdots, d_n \}$，以及在所有文本中出现的$m$$m$个单词的集合$W=\{w_1,w_2,\cdots ,w_m\}$$W = \{w_1, w_2, \cdots, w_m \}$。将单词在文本中出现的数据用一个单词-文本矩阵表示，记作$X$$X$：

元素$x_{ij}$$x_{ij}$表示单词$w_i$$w_{i}$在文本$d_j$$d_j$中出现的频数或权值。

权值一般使用单词频率-逆文本频率（TF-IDF）表示，其定义如下：

直观上讲，一个单词在文本中出现的频数越高，该单词在该文本中的重要度越高，含有该单词的文本数越少，该单词越能表示其所在文本的特点。

单词向量空间模型直接使用单词-文本矩阵的信息。每个列向量可以看成该文本的单词向量表示形式，可以使用余弦相似度计算不同文本之间的相似度。该模型的优点是模型简单，计算效率高，缺点是对一词多义或多词一义未必能够准确表达。

话题向量空间

话题向量空间

假设所有文本共有$k$$k$个话题，每个话题由一个$m$$m$维的向量表示，单词-话题矩阵$T$$T$的表示如下：

文本在话题向量空间的表示

定义矩阵$Y$$Y$表示话题在文本中出现的情况，称为话题-文本矩阵，记作：

单词向量空间->话题向量空间

单词-文本矩阵$X$$X$可以近似地表示为单词-话题矩阵$T$$T$与话题-文本矩阵$Y$$Y$的乘积形式，即：

下图示意性地表示实现潜在语义分析的矩阵因子分解过程：

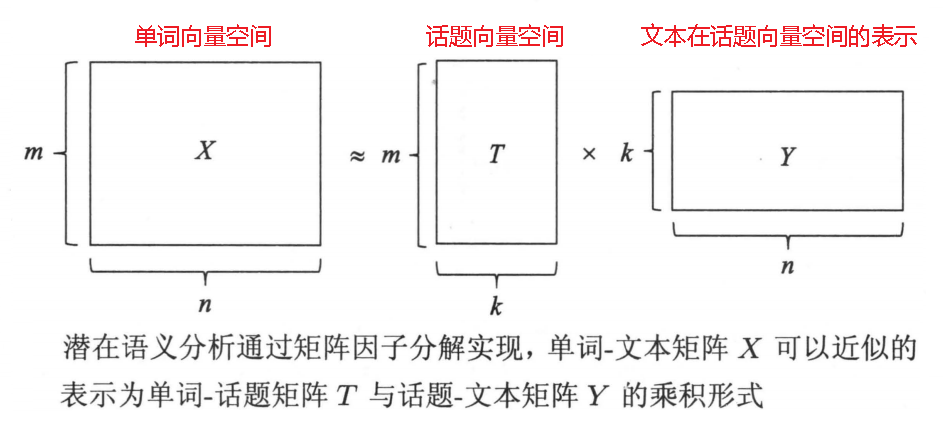
LSA分析算法

SVD分解

对单词-文本矩阵$X$$X$进行SVD分解，将其左矩阵作为话题向量空间，将其对角矩阵与右矩阵的乘积作为文本在话题向量空间的表示。具体如下述公式表示：

非负矩阵分解

对单词-文本矩阵$X$$X$进行非负矩阵分解，将其左矩阵作为话题向量空间，将其右矩阵作为文本在话题向量空间的表示。