PLSA2022-10-12

前置知识概率公式独立随机变量的性质PLSA简介PLSA模型生成模型共现模型总结PLSA的学习方法生成模型定义对数似然函数E步：定义Q函数M步：极大化Q函数总结共现模型参考文档

前置知识

概率公式

加法公式
$\begin{matrix} (1) & P (X) = \sum_{Y} P (X, Y) \end{matrix}$
乘法公式
$\begin{matrix} (2) & \begin{aligned} P (X, Y) & = P (X ∣ Y) P (Y) \\ = P (Y ∣ X) P (X) \end{aligned} \end{matrix}$
贝叶斯公式

\begin{matrix} (3) & \begin{aligned} P (Y ∣ X) & = \frac{P (X, Y)}{P (X)} \\ = \frac{P (X ∣ Y) P (Y)}{\sum_{Y} P (X, Y)} \\ = \frac{P (X ∣ Y) P (Y)}{\sum_{Y} P (X ∣ Y) P (Y)} \end{aligned} \end{matrix}

独立随机变量的性质

$X$ $Y$ 独立，那么：

\begin{matrix} (4) & P (X, Y) = P (X) P (Y) \end{matrix}

根据乘法公式：

\begin{matrix} (5) & P (X, Y) = P (X ∣ Y) P (Y) \end{matrix}

因此：

\begin{matrix} (6) & P (X) = P (X ∣ Y) \end{matrix}

PLSA简介

概率潜在语义分析（probabilistic latent semantic analysis，PLSA），是一种利用概率生成模型对文本集合进行话题分析的无监督学习方法。模型的特点是使用隐变量表示话题，模型的过程为文本生成话题，话题生成单词，从而得到单词-文本共现数据。假设每个文本由一个话题分布决定，每个话题由一个单词分布决定。

PLSA模型

PLSA有生成模型，以及等价的共现模型。

生成模型

假设有如下集合：

单词集合
$W = \{w_1, w_2, \cdots, w_M \}$ $M$ 为单词个数
文本集合
$D = \{d_1, d_2, \cdots, d_N \}$ $N$ 为文本个数
话题集合
$Z = \{z_1, z_2, \cdots, z_K \}$ $K$ 为话题个数

$w$ $d$ $z$ 取值于话题集合。定义如下概率分布（都是多项式分布）：

$\operatorname{P}(d)$ $d$ 的概率
$\operatorname{P}(z \mid d)$ $d$ $z$ 的概率
$\operatorname{P}(w \mid z)$ $z$ $w$ 的概率

生成模型通过以下步骤生成文本-单词共现数据：

$\operatorname{P}(d)$ $d$ $N$ 个文本。针对每个文本，执行以下操作：
$d$ $\operatorname{P}(z \mid d)$ $z$ $L$ $L$ 是文本长度；
$z$ $\operatorname{P}(w \mid z)$ $w$ 。

$w$ $d$ $z$ $(w, z, d)$ $(w, d)$ $(w, d)$ $\mathbf{T}$ $(w,d)$ 的出现次数。

$\mathbf{T}$ $(w,d)$ 的生成概率的乘积：

\begin{matrix} (7) & \begin{matrix} P (T) = \prod_{(w, d)} P (w, d)^{n (w, d)} \\ 其 中 ， n (w, d) 为 (w, d) 出 现 的 次 数 \end{matrix} \end{matrix}

$z$ $w$ $d$ 条件独立，即：

\begin{matrix} (8) & \begin{aligned} P (w, z ∣ d) & = P (z ∣ d) P (w ∣ z, d) \\ = P (z ∣ d) P (w ∣ z) \end{aligned} \end{matrix}

$(w,d)$ 的生成概率由以下公式决定：

\begin{matrix} (9) & \begin{aligned} P (w, d) & = P (d) P (w ∣ d) \\ = P (d) \sum_{z} P (z ∣ d) P (w ∣ z, d) \\ = P (d) \sum_{z} P (z ∣ d) P (w ∣ z) \end{aligned} \end{matrix}

上式即为生成模型的定义。

生成模型属于概率有向图模型，可以用有向图表示。如下图所示，实心圆表示观测变量，空心圆表示隐变量，箭头表示概率依存关系多次重复 $(N和L)$ 表示重复的次数。

PLSA

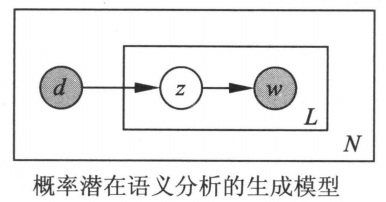
共现模型

$\mathbf{T}$ $(w,d)$ 的生成概率的乘积：

\begin{matrix} (10) & \begin{matrix} P (T) = \prod_{(w, d)} P (w, d)^{n (w, d)} \\ 其 中 ， n (w, d) 为 (w, d) 出 现 的 次 数 \end{matrix} \end{matrix}

$z$ $w$ $d$ 条件独立，即：

\begin{matrix} (11) & P (w, d ∣ z) = P (w ∣ z) P (d ∣ z) \end{matrix}

$(w,d)$ 的概率由以下公式决定：

\begin{matrix} (12) & \begin{aligned} P (w, d) & = \sum_{z} P (w, d, z) \\ = \sum_{z} P (z) P (w, d ∣ z) \\ = \sum_{z} P (z) P (w ∣ z) P (d ∣ z) \end{aligned} \end{matrix}

上式即为共现模型的定义。

$d$ $w$ $z$ 为隐变量

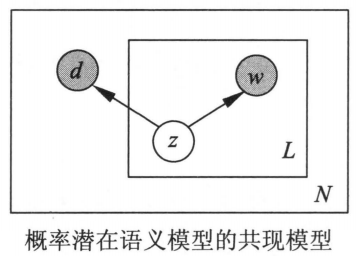
PLSA_共现

总结

$w$ $d$ $w$ $d$ 是对称的。因此，前者称为非对称模型，后者称为对称模型。

PLSA的学习方法

生成模型

定义对数似然函数

优化目标是对数似然函数最大化，该函数定义如下：

\begin{matrix} (13) & \begin{aligned} \log P (T) & = \log \prod_{i, j} P (w_{i}, d_{j})^{n (w_{i}, d_{j})} \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log P (w_{i}, d_{j}) \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log [P (d_{j}) \sum_{k = 1}^{K} P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})] \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) [\log P (d_{j}) + \log \sum_{k = 1}^{K} P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})] \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log P (d_{j}) + \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log \sum_{k = 1}^{K} P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k}) \end{aligned} \end{matrix}

$n(w_i, d_j)$ $\log \operatorname{P}(d_j)$ 都为常数，因此，将对数似然函数简化为：

\begin{matrix} (14) & \log P (T) = L = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log \sum_{k = 1}^{K} P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k}) \end{matrix}

E步：定义Q函数

根据Jesson不等式：

\begin{matrix} (15) & \log \sum p \cdot f (x) \geq \sum p \cdot \log f (x) \end{matrix}

$\operatorname{P}(z_k \mid w_i, d_j)$ ，对于对数似然函数：

\begin{matrix} (16) & \begin{aligned} L & = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log \sum_{k = 1}^{K} P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k}) \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \log \sum_{k = 1}^{K} \frac{P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})}{P (z_{k} ∣ w_{i}, d_{j})} \cdot P (z_{k} ∣ w_{i}, d_{j}) \\ \geq \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} P (z_{k} ∣ w_{i}, d_{j}) \log \frac{P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})}{P (z_{k} ∣ w_{i}, d_{j})} \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} P (z_{k} ∣ w_{i}, d_{j}) {\log [P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})] - \log P (z_{k} ∣ w_{i}, d_{j})} \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} {P (z_{k} ∣ w_{i}, d_{j}) \log [P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})] - P (z_{k} ∣ w_{i}, d_{j}) \log P (z_{k} ∣ w_{i}, d_{j})} \end{aligned} \end{matrix}

$\operatorname{P}(z_k \mid w_i, d_j)$ 为常数，因此上式可简化为：

\begin{matrix} (17) & \begin{aligned} L & \geq \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} P (z_{k} ∣ w_{i}, d_{j}) \log [P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})] \end{aligned} \end{matrix}

$Q$ 函数为：

\begin{matrix} (18) & Q = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} P (z_{k} ∣ w_{i}, d_{j}) \log [P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})] \end{matrix}

$Q$ $L$ $L$ $Q$ 的极大化问题。

$\operatorname{P}(z_k \mid w_i, d_j)$ 化简为：

\begin{matrix} (19) & \begin{aligned} P (z_{k} ∣ w_{i}, d_{j}) & = \frac{P (z_{k}, w_{i}, d_{j})}{P (w_{i}, d_{j})} \\ = \frac{P (z_{k}) P (w_{i}, d_{j} ∣ z_{k})}{P (w_{i}, d_{j})} \\ = \frac{P (z_{k}) P (d_{i} ∣ z_{k}) P (w_{i} ∣ z_{k})}{P (w_{i}, d_{j})} \\ = \frac{P (d_{j}) P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})}{\sum_{a = 1}^{K} P (w_{i}, d_{j}, z_{a})} \\ = \frac{P (d_{j}) P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})}{\sum_{a = 1}^{K} P (d_{j}) P (z_{a} ∣ d_{j}) P (w_{i} ∣ z_{a})} \\ = \frac{P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})}{\sum_{a = 1}^{K} P (z_{a} ∣ d_{j}) P (w_{i} ∣ z_{a})} \end{aligned} \end{matrix}

$Q$ 函数可以化简为：

\begin{matrix} (20) & \begin{aligned} Q & = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} P (z_{k} ∣ w_{i}, d_{j}) \log [P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})] \\ = \sum_{i = 1}^{M} \sum_{j = 1}^{N} n (w_{i}, d_{j}) \sum_{k = 1}^{K} \frac{P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})}{\sum_{a = 1}^{K} P (z_{a} ∣ d_{j}) P (w_{i} ∣ z_{a})} \log [P (z_{k} ∣ d_{j}) P (w_{i} ∣ z_{k})] \end{aligned} \end{matrix}

$\operatorname{P}(w_i \mid z_k)$ $\operatorname{P}(z_k \mid d_j)$ 为变量，即待求解参数。

M步：极大化Q函数

$Q$ $\operatorname{P}(w_i \mid z_k)$ $\operatorname{P}(z_k \mid d_j)$ 为概率分布，因此：

\begin{matrix} (21) & \begin{matrix} \sum_{i = 1}^{M} P (w_{i} ∣ z_{k}) = 1, k = 1, 2, \dots, K \\ \sum_{k = 1}^{K} P (z_{k} ∣ d_{j}) = 1, j = 1, 2, \dots, N \end{matrix} \end{matrix}

$\tau _k$ $\rho _j$ $\Lambda$ ：

\begin{matrix} (22) & Λ = Q + \sum_{k = 1}^{K} τ_{k} (1 - \sum_{i = 1}^{M} P (w_{i} ∣ z_{k})) + \sum_{j = 1}^{N} ρ_{j} (1 - \sum_{k = 1}^{K} P (z_{k} ∣ d_{j})) \end{matrix}

$\Lambda$ $\operatorname{P}(w_i \mid z_k)$ $\operatorname{P}(z_k \mid d_j)$ 求偏导，并令其为0，得：

\begin{matrix} (23) & \begin{aligned} \sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} ∣ w_{i}, d_{j}) - τ_{k} P (w_{i} ∣ z_{k}) = 0, i = 1, 2, \dots, M; k = 1, 2, \dots, K \\ \sum_{i = 1}^{M} n (w_{i}, d_{j}) P (z_{k} ∣ w_{i}, d_{j}) - ρ_{j} P (z_{k} ∣ d_{j}) = 0, j = 1, 2, \dots, N; k = 1, 2, \dots, K \end{aligned} \end{matrix}

解方程组，得到M步的参数估计公式：

\begin{matrix} (24) & \begin{aligned} P (w_{i} ∣ z_{k}) & = \frac{\sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} ∣ w_{i}, d_{j})}{\sum_{m = 1}^{M} \sum_{j = 1}^{N} n (w_{m}, d_{j}) P (z_{k} ∣ w_{m}, d_{j})} \\ P (z_{k} ∣ d_{j}) & = \frac{\sum_{i = 1}^{M} n (w_{i}, d_{j}) P (z_{k} ∣ w_{i}, d_{j})}{n (d_{j})} \end{aligned} \end{matrix}

总结

$\mathbf{EM}$ 算法：

$W=\{w_1, w_2, \cdots, w_M \}$ $D = \{d_1, d_2, \cdots, d_N \}$ $Z = {z_1, z_2, \cdots, z_K}$ $n(w_i, d_j), i=1,2,\cdots,M, \quad j=1,2,\cdots, N$ 。

$\operatorname{P}(w_i \mid z_k)$ $\operatorname{P}(z_k \mid d_j)$

步骤：

$\operatorname{P}(w_i \mid z_k)$ $\operatorname{P}(z_k \mid d_j)$ 的初始值

（2）迭代执行E步和M步，直到收敛为止。

E步：

\begin{matrix} (25) & P (z_{k} ∣ w_{i}, d_{j}) = \frac{P (w_{i} ∣ z_{k}) P (z_{k} ∣ d_{j})}{\sum_{k = 1}^{K} P (w_{i} ∣ z_{k}) P (z_{k} ∣ d_{j})} \end{matrix}

M步：

\begin{matrix} (26) & \begin{aligned} P (w_{i} ∣ z_{k}) & = \frac{\sum_{j = 1}^{N} n (w_{i}, d_{j}) P (z_{k} ∣ w_{i}, d_{j})}{\sum_{m = 1}^{M} \sum_{j = 1}^{N} n (w_{m}, d_{j}) P (z_{k} ∣ w_{m}, d_{j})} \\ P (z_{k} ∣ d_{j}) & = \frac{\sum_{i = 1}^{M} n (w_{i}, d_{j}) P (z_{k} ∣ w_{i}, d_{j})}{n (d_{j})} \end{aligned} \end{matrix}

共现模型

暂略。