Word2Vec2021-10-16
背景知识
Log-linear Model
定义(Log Linear Models):将语言模型的建立看成是一个多分类问题,相当于线性分类器加上softmax操作。
符号定义
- 单词:
- 词典:,其中,为单词个数。由单词组成的集合。
- 语料库:,由单词组成的文本序列。
- 上下文:是单词在语料库中前个单词和后个单词组成的文本序列,称为中心词,为窗口长度
- 词向量:表示单词对应的词向量
两种模型
Word2Vec简介
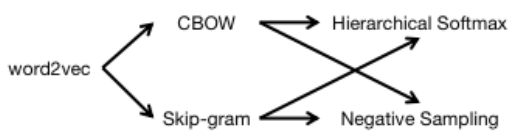
语言模型基本思想:句子中下一个词的出现和前面的词是有关系的,所以可以使用前面的词预测下一个词。
Word2Vec基本思想:句子中相近的词之间是有联系的,比如今天后面经常出现上午、下午。所以Word2Vec的基本思想就是用词来预测词,CBOW使用周围词预测中心词,Skip-gram使用中心词预测周围词。
单个词到单个词
为了便于理解CBOW和Skip-gram模型,先介绍一个词到一个词的简单模型。
假设输入为:我喜欢观看巴西足球世界杯。经过分词,得到词表:['我','喜欢','观看','巴西','足球','世界杯']。为了构建一个词到一个词的模型,将单词两两分组,得到数据集:[['我','喜欢'],['喜欢','观看'],['观看','巴西'],['巴西','足球'],['足球','世界杯']]。使用one-hot对单词进行表示如下图所示:
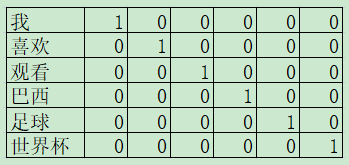
接下来,输入数据:['我', '喜欢'],在输出中,期望'喜欢'的概率最大。
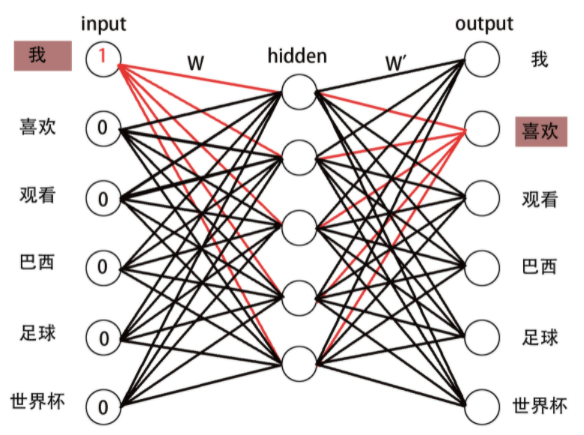
扩展到一般的网络结构:
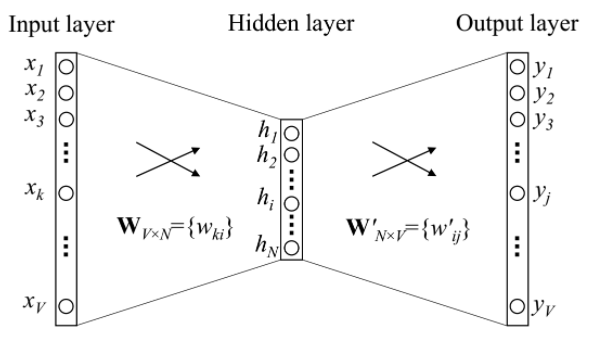
定义如下符号:
- :词表大小(或语料库中不同单词的数目)
- :词向量维度
- :输入单词,使用one-hot编码表示
- :原始单词
- :单词的第个周围词,其中,
- :输入层与隐藏层之间的权重
- :隐藏层与输出层之间的权重
- :每个单词的预测值,通过softmax计算可得到概率
- :每个单词的概率
前向计算:
,注意,出现在每一个当中,如果对求导,需要遍历每一个
损失函数:
给定中心词,预测词的概率
损失函数
假设是正确的单词对应的索引,我们期望最大,等价地,可以导出如下损失函数:
反向传播:
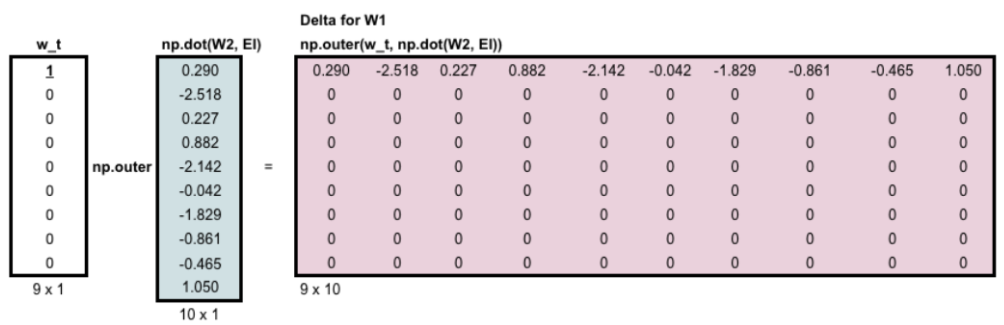
对求导对求导,得到的矩阵,由于只有行非,所以矩阵只有行非,为其中, 参数更新:
更新:需要更新整个矩阵
更新:只需要更新对应的行。梯度更新如下图所示:(注:应为,应为)
CBOW
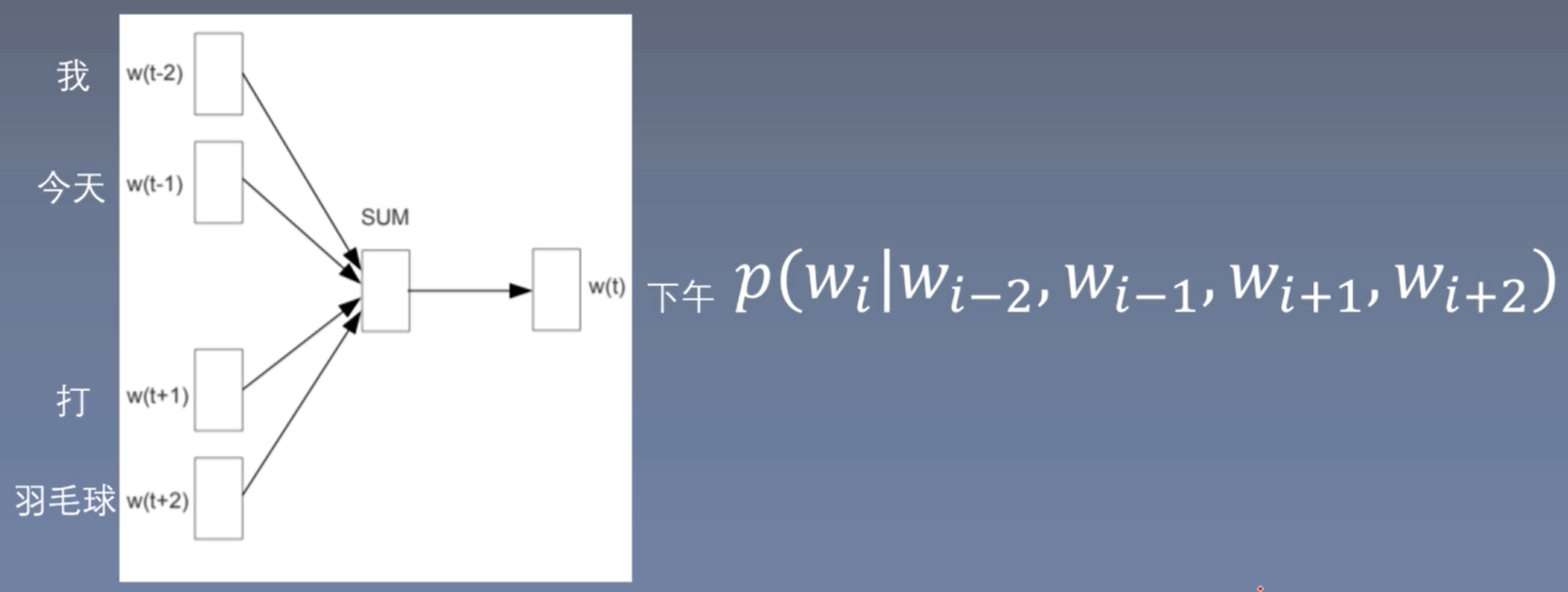
首先,需要定义window,即选取多少个周围词,上图中window=2。通过周围词预测中心词,该问题为多分类问题。
词向量:
输入:周围词,,将其词向量相加得到周围词词向量
标签:中心词,,为语料库中的中心词个数
使用向量内积表示词向量的相似度,那么,中心词的预测概率为:
其中,、为中心词的词向量 损失函数(使中心词的概率最大):
其中,为中心词个数,为中心词,为对应的周围词,为周围词词向量的和,为中心词词向量
Skip-gram
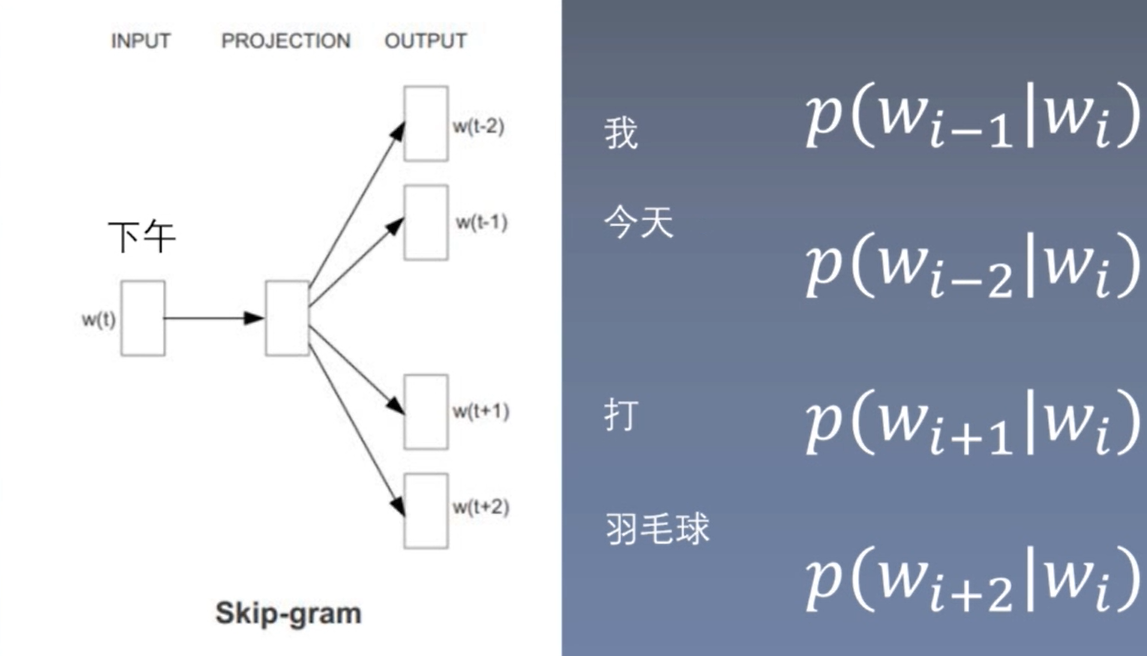
首先,需要定义window,即选取多少个周围词,上图中window=2。通过中心词预测周围词,该问题为多分类问题。
词向量:
输入:中心词,
标签:周围词,,为周围词个数
使用向量内积表示词向量的相似度,那么,周围词的预测概率为:
其中,为周围词的词向量 损失函数(使周围词的概率最大):
其中,为窗口大小
计算优化
为了解决上述模型中softmax计算量太大的问题,使用以下两种方法进行优化。
Hierarchical softmax
核心思想:将多分类问题转化为多个二分类问题。
方法:将词表中的单词,按照频率构建一颗哈夫曼树,这样,对每一个单词,便有了唯一正确的一个搜索路径。如果将搜索路径视为输入,将单词视为真实标签,那么,从根结点到目标单词(叶子结点),便是若干个二分类过程。至此,完成了问题的转化。
CBOW
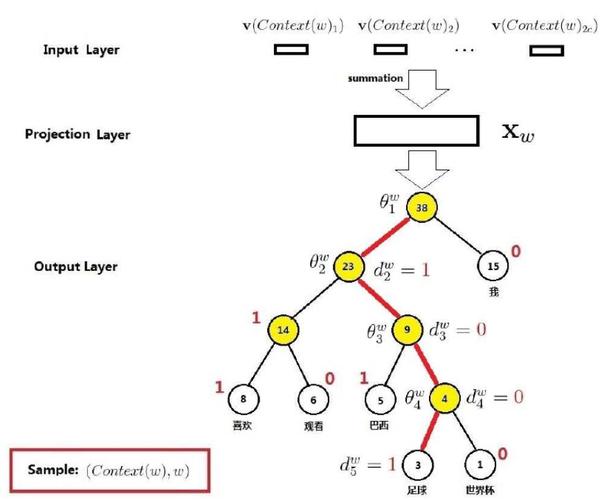
针对上述哈夫曼树,各层解释如下:
输入层
,,,,其中,为单词的向量化表示
投影层
输出层
给定的周围词,单词出现的概率,即
为方便计算损失函数,定义如下变量:
路径:
从根结点出发,到达对应的叶子结点的路径。其中,为路径长度,即路径中结点数目;为路径中的结点,为根结点,为对应的叶子结点。
编码:
的Huffman编码。其中,为路径中第个结点对应的编码(根结点不对应编码)。
权值:
路径中非叶子结点对应的参数向量。其中,为路径中第个非叶子结点对应的参数向量。
那么,在已知周围词的条件下,中心词的概率为:
注:顺着路径走 其中,
注:该概率决定往左还是往右 该概率也可以写成如下形式:
那么,似然函数为:
对数似然函数为:
对数似然函数关于求偏导为:
所以,的更新公式为:
其中,为学习率 对数似然函数关于求偏导为:
的更新公式为:
其中, Skip-gram
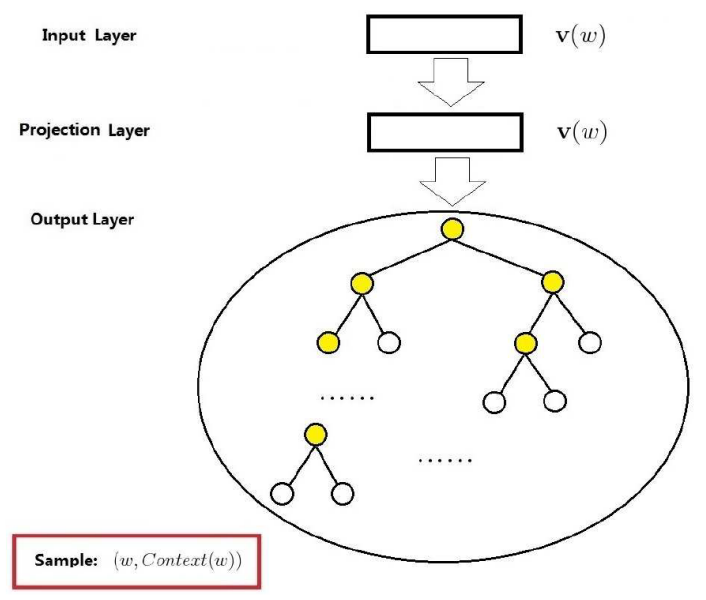
针对上述哈夫曼树,各层解释如下:
输入层
当前样本的中心词对应的词向量
映射层
恒等映射,多余,为了和CBOW模型的网络结构进行对比。
输出层
那么,给定中心词的条件下,其周围词的条件概率为:
其中,
并且:
所以,似然函数为:
对数似然函数为:
对数似然函数关于的偏导为:
的更新公式为:
其中,为学习率 对数似然函数关于的偏导为:
的更新为:
Negative Sampling
CBOW
设的负样本子集(非的周围词)为:
对于,定义表示词的标签,即是否是中心词的周围词,正样本标签为1,负样本标签为0:
在给定周围词的条件下,中心词与负样本数据集,即,其似然函数为:
其中,
其中,为词向量之和,为模型参数 上式也可以写为:
关于词表的对数似然函数为:
对数似然函数关于的偏导为:
参数的更新公式为:
对数似然函数关于的偏导为:
参数的更新公式为:
其中,
Skip-gram
给定中心词,对应多个周围词,表示相对于的负样本。
给定周围词,的似然函数为:
其中,为处理周围词时生成的负样本子集 其中,
上式又可以写为:
关于词表的对数似然函数为:
对数似然函数关于的偏导为:
参数的更新公式为:
对数似然函数关于的偏导为:
参数的更新公式为:
采样
负采样
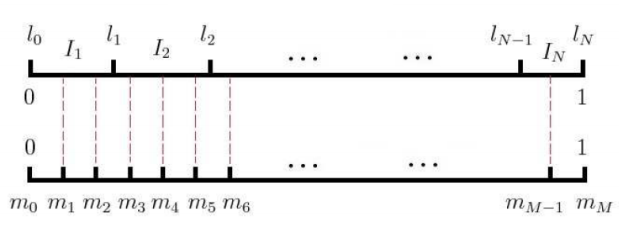
非等距剖分:
设词典中单词对应的线段为,其长度为:
其中,为词在语料中的出现次数 可将线段拼接为长度为1的单位线段。记:
则以为剖分点可得到区间上的一个非等距剖分:
等距剖分:
在区间上以剖分点做等距剖分,其中。
等距与非等距映射:
将等距剖分的内部点投影到非等距剖分,则可建立与区间的映射,进一步建立与词之间的映射。
重采样
重采样的目的:提高低频次出现的频率,降低高频词出现的概率。
训练集中的词会以的概率被删除,概率计算公式为:
其中,为词在数据集中出现的频率,论文中取 复杂度分析
使用模型参数量表征模型复杂度。
定义符号:
:训练复杂度
:迭代次数
:数据集大小
:参与本次计算的参数的数目
那么:
NNLM(前馈神经网络)
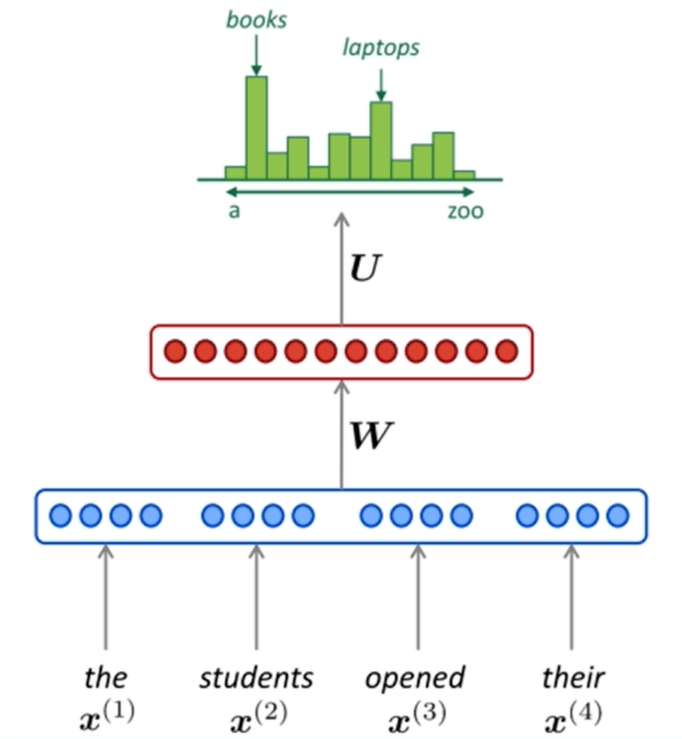
模型:使用前个词预测下一个词
其中, 符号定义:
- :上文词(训练数据)个数
- :词向量维度
- :词表的大小
- :隐藏层大小
参数个数:
输入层:
隐藏层:
输出层:。如果使用HS对输出进行优化,则需要进行次二分类,参数的长度为,故参数量为
总参数量:
RNNLM(循环神经网络语言模型)
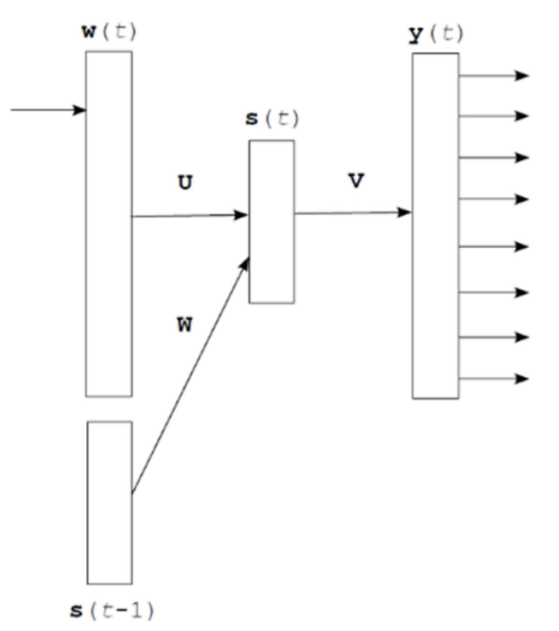
其中,表示时刻的当前输入单词的词向量,代表隐藏层的前一次输出 符号定义:
- :维度为
- :维度为
- :维度为
复杂度计算:
输入层:
隐藏层:
输出层:
总复杂度:假设
Skip-gram
符号定义:
- :中心词个数
- :词向量维度
- :单词个数
原始复杂度:
- 输入:
- 输出:通过矩阵进行计算得到,再通过softmax操作得到最终结果。因此,本次参与计算的参数个数为
- 总复杂度:
Hierarchical softmax复杂度:
- 次二分类,参数的长度为,故复杂度为
Negative Sampling复杂度:
- 正样本个数为,负样本个数为,词向量维度为,故总的复杂度为
CBOW
周围词个数为,每个词的向量维度为,所以输入的参数量为。经过sum操作,得到汇总的词向量,维度为,再经过权重矩阵计算,得到最终预测结果。所以输出层的参数量为。
原始复杂度:
HS复杂度:
NEG复杂度:
复杂度总结
如下对各模型复杂度进行总结:
- NNLM:
- RNNLM:
- Skip_gram+HS:
- Skip_gram+NEG:
- CBOW+HS:
- CBOW+NEG:
问题
为什么可以使用向量内积度量相似度?
,其中,为两向量的夹角。如果向量已被单位化,那么向量内积等于,此时,两向量越接近,夹角越小,内积越大。
对比Skip-gram和CBOW。训练速度上CBOW更快;对低频词,Skip-gram效果更好,因为Skip-gram是用当前词预测上下文,当前词是低频还是高频没有区别,但是CBOW相当于是完形填空,更倾向于选择常见的词而不是低频词。总体上讲,Skip-gram模型的效果更好。
参考链接
https://spaces.ac.cn/archives/4122
源码 GitHub - tmikolov/word2vec: Automatically exported from code.google.com/p/word2vec
Embedding从入门到专家必读的十篇论文 - 知乎 (zhihu.com)
词向量模型word2vector详解 - 空空如也_stephen - 博客园 (cnblogs.com)
word2vec公式推导及python简单实现 - Kayden_Cheung - 博客园 (cnblogs.com)
Python implementation of Word2Vec | Marginalia (claudiobellei.com)
The backpropagation algorithm for Word2Vec | Marginalia (claudiobellei.com)
word2vec公式推导及python简单实现 - Kayden_Cheung - 博客园 (cnblogs.com)
深度之眼:NLP-baseline 体验课 (deepshare.net)
七月在线:补充视频:陈博士带你从头到尾通透word2vec (julyedu.com)
【机器学习】白板推导系列(三十六) ~ 词向量(Word Vector)哔哩哔哩bilibili
【双语字幕】斯坦福CS224n《深度学习自然语言处理》课程(2019) by Chris Manning哔哩哔哩bilibili











